목차
문제 출처 : https://www.acmicpc.net/problem/17611
17611번: 직각다각형
입력의 첫 줄에는 단순직각다각형의 꼭지점의 개수를 나타내는 정수 n(4 ≤ n ≤ 100,000)이 주어지고, 이어지는 n개 줄 각각에 단순직각다각형 꼭지점의 좌표 (xi, yi)가 차례대로 주어진다. 주어지
www.acmicpc.net
이 문제는 2019년 정보올림피아드 1차 대회 중등부 2번 문제 입니다.
문제 이해하기
수평, 수직을 체크하며 가장 겹치는 부분이 많은 곳을 찾는 문제 입니다. 예제 2번을 보며 같이 생각해 보겠습니다. 예제 2번의 좌표를 찾아 표시하면 다음과 같습니다.

가장 겹치는 점이 많은 것은 수평 선분일 때 6개이고, 수직 선분은 2개 입니다. 따라서 출력값은 max(6, 2)로 6이 출력 됩니다. 이렇게 직각 다각형을 그려서 선분이 겹치는 부분이 몇개나 되는지 찾는다면 시간초과가 날 수 밖에 없습니다.
이 문제에서 가장 큰 힌트는 이 도형이 직각 다각형이라는 것입니다. 무슨 뜻이냐면 한 번 x축이 변경되면 다음에는 y축이 변경되고, 그 다음은 다시 x축이 변경됩니다. 즉 번갈아가면서 변화가 생기기 때문에 이 부분을 잘 이용하면 문제를 쉽게 해결할 수 있습니다.
먼저 수직 선분 V를 생각해 보겠습니다. 이 V 값은 y축 값은 아무 영향을 끼치지 않습니다. 오직 x축의 값의 변화량에 따라서 겹치는 부분이 생깁니다. x축의 변화량을 보겠습니다. 0 → 1 → 2 → 5 → 4 → 3 → 0으로 변합니다. 마지막 0은 직각 다각형을 그리기 위해서는 원점인 0으로 돌아와야 하기 때문 입니다. 이것을 그림으로 표현하면 다음과 같습니다.
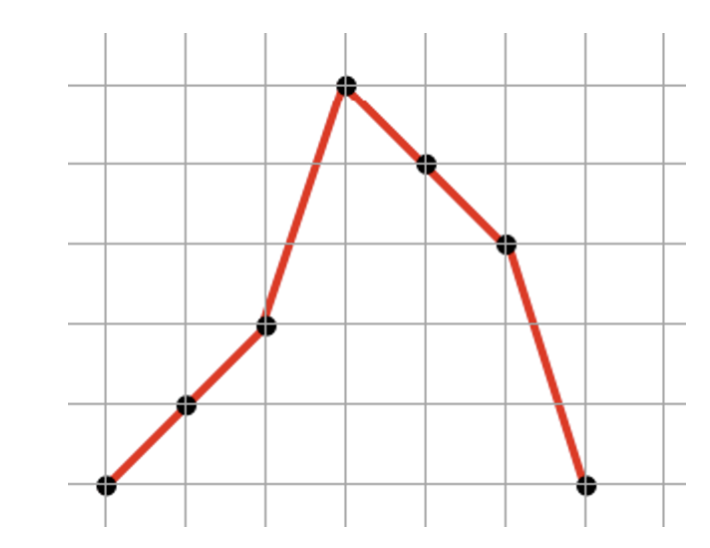
여기에 수평한 선분을 그으면 2개만 겹치게 그릴 수 있습니다. 좀 더 복잡한 수평 선분 H를 생각해 보겠습니다.
| 0 → 3 → 1 → 3 → 0 → 2 → 0 |
위 순서로 변경되고 이것을 그래프로 표현하면 아래와 같습니다.

여기에 수평한 선분을 그으면 총 6개의 겹치는 부분이 생기게 됩니다.
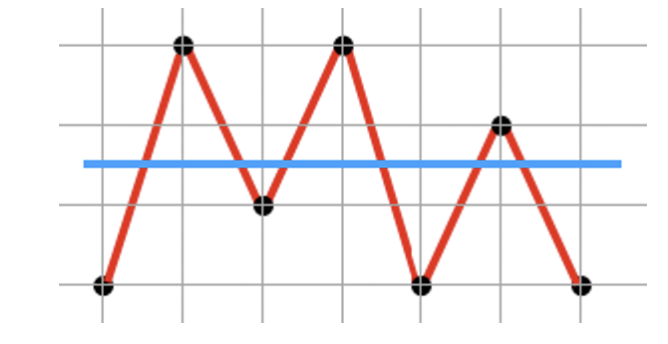
이제 우리는 직각 다각형을 생각할 필요 없이 좌표의 변화량을 따져가며 가장 큰 변화량이 있는 부분만 찾으면 된다는 사실을 알았습니다. 값이 좌표로 주어지기 때문에 낮은 값은 더해주고, 높은 값을 빼주면서 합계를 따져보겠습니다. 0에서부터 3까지 선분이 있으니 line[0] = 1, line[3] = -1을 해줍니다.
| 0 | 1 | 2 | 3 |
| 1 | 0 | 0 | -1 |
다음으로 3에서 1까지 입니다. line[3] = -2가 되고, line[1] = 1이 됩니다.
| 0 | 1 | 2 | 3 |
| 1 | 1 | 0 | -2 |
이번에는 앞선 이동과 반대로 움직여 1에서 3까지 이동 합니다.
| 0 | 1 | 2 | 3 |
| 1 | 2 | 0 | -3 |
3에서 0으로 떨어졌습니다.
| 0 | 1 | 2 | 3 |
| 2 | 2 | 0 | -4 |
다음으로 0에서 2까지 올라갔습니다.
| 0 | 1 | 2 | 3 |
| 3 | 2 | -1 | -4 |
마지막으로 2에서 0으로 떨어졌습니다.
| 0 | 1 | 2 | 3 |
| 4 | 2 | -2 | -4 |
겹치는 부분이 늘어나는 부분과 줄어드는 부분이 어디인지 알 수 있습니다. 0에서 1사이에 있으면 총 4개의 겹치는 부분이 있습니다. 1에서 2 사이에는 겹치는 부분이 2개 더 늘어나 총 6개가 됩니다. 2에서 3 사이라면 꺽이는 부분이 생겨 겹치는 부분이 4개로 줄어 듭니다. 마지막으로 3보다 크게 되면 겹치는 부분이 없어 0이 됩니다.
여기서는 마지막이 시작 지점인 0이라 문제 없지만 0이 아닌 경우에는 한 번 더 0으로 이동하는 코드를 넣어주어야 합니다.
그리고 점의 범위를 보면 -500,000부터 500,000 까지 입니다. 리스트는 음수를 표현할 수 없기 때문에 범위를 맞추기 위해 각 좌표에 500,000을 더해줍니다. 그럼 음수가 되는 부분이 없이 표현이 가능합니다.
코드 작성하기
그럼 코드를 직접 작성해 보겠습니다.
입력 받기
N = int(input())
arr = []
for _ in range(N):
x, y = map(int, input().split())
arr.append((x, y))
꼭지점의 개수 N과 꼭지점의 좌표를 입력받아 arr이라는 리스트에 넣었습니다.
결과 출력
H, V = 0, 1
ans = max(solve(H), solve(V))
print(ans)
겹치는 부분을 찾는 함수 slove를 만들었습니다. solve 함수는 아래에 따로 구현 하도록 하겠습니다. 각각 수평과 수직에서 겹치는 부분을 찾는 함수 입니다. H를 입력하면 수평을, V를 입력하면 수직을 체크하도록 하였습니다.
solve 함수
MID = 500_000
TOTAL = MID * 2 + 1
def solve(hv):
line = [0] * TOTAL
for cur in range(hv, N, 2):
nxt = (cur + 1) if cur + 1 != N else 0
j = 0
if arr[cur][0] == arr[nxt][0]:
j = 1
min_p, max_p = sorted([arr[cur][j], arr[nxt][j]])
line[min_p + MID] += 1
line[max_p + MID] -= 1
ans, tot = 0, 0
for i in line:
tot += i
ans = max(ans, tot)
return ans
이 문제의 핵심이라 할 수 있는 solve 함수 입니다. 먼저 리스트의 범위로 인해 500,000을 더해주어야 합니다. MID라는 변수를 통해 이 값을 저장 합니다. 다음으로 리스트의 크기는 500,000을 더해준 1,000,000이 됩니다. 여기에 1을 더해주어 해당 값까지 사용할 수 있게 하였습니다.
solve 함수는 수평, 수직 두 번 동작을 합니다. 예제 입력을 보면 알 수 있듯이 첫 번째 값이나 두 번째 값이 2개씩 일치합니다. x축을 기준으로 y값이 변하던가, y축을 기준으로 x값이 변하기 때문 입니다. 앞의 값 cur과 뒤의 값 nxt의 0번째인 x축이 같으면 y값인 1번째를 확인하고, y축이 같으면 x값인 0번째를 확인하도록 j값을 세팅 합니다. 이 때 nxt 값이 N이 될 수 있습니다. 총 N이 10이라면 cur이 9가 최대가 될 것이고 nxt 값이 10이 될 수 있기 때문 입니다. 그럼 맨 첫 번째 위치로 돌아오게 하기 위해 cur + 1 == N이면 0이 되게 하였습니다.
이제 cur, nxt 두 값을 입력 받아 작은 값은 1을 더하고, 큰 값은 1을 빼주었습니다.
마지막으로 line값을 확인하며 가장 큰 tot 값을 찾습니다. 이 최대로 큰 tot값이 ans가 되고, 그 값을 리턴합니다.
전체 코드
N = int(input())
arr = []
for _ in range(N):
x, y = map(int, input().split())
arr.append((x, y))
MID = 500_000
TOTAL = MID * 2 + 1
H, V = 0, 1
def solve(hv):
line = [0] * TOTAL
for cur in range(hv, N, 2):
nxt = (cur + 1) if cur + 1 != N else 0
j = 0
if arr[cur][0] == arr[nxt][0]:
j = 1
min_p, max_p = sorted([arr[cur][j], arr[nxt][j]])
line[min_p + MID] += 1
line[max_p + MID] -= 1
ans, tot = 0, 0
for i in line:
tot += i
ans = max(ans, tot)
return ans
ans = max(solve(H), solve(V))
print(ans)
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 19940] 2020 정올 1차 초등부 "피자 오븐"(1) (0) | 2024.03.03 |
|---|---|
| [백준 19942] 2020 정올 1차 중등부 "다이어트" (0) | 2024.03.03 |
| [백준 17613] 2019 정올 1차 고등부 "점프" (1) | 2024.02.29 |
| [백준 17610] 2019 정올 1차 중등부 "양팔저울" (0) | 2024.02.23 |
| [백준 17612] 2019 정올 1차 고등부 "쇼핑몰" (0) | 2024.02.22 |

