목차
완전 순열(Complete permutation) 또는 교란(derangement) 순열이라 불리는 순열에 대해 알아보겠습니다. 교란 순열의 예를 들어 보겠습니다.
교란 순열이란?
졸업을 맞이하여 서로를 축하하기 위해 친구 N명이 각자 선물 하나씩을 준비하였습니다. 선물을 내려놓고 아무거나 하나씩 집었을 때 자신의 선물이 아닌 다른 사람의 선물을 선택 할 경우의 수를 교란 순열이라고 합니다. 선물을 아무거나 고르는 경우의 수는 N!로 쉽게 구할 수 있습니다. 하지만 자신의 선물을 고르지 않는 경우에는 다른 방식으로 문제를 해결해야 합니다.
친구가 1명일 때
먼저 친구가 1명 있다고 생각하겠습니다. 한 명이 선물을 고른다면 어떻게 해도 자기 자신의 선물을 고를 수 밖에 없습니다. 따라서 경우의 수는 0 입니다. 이것을 아래와 같은 식으로 표현하겠습니다.
D(1) = 0
친구가 2명일 때
다음으로 친구 2명이 있는 경우를 생각하겠습니다. 두 사람이 선물을 교환하는 방법은 하나밖에 없습니다.
D(2) = 1

친구가 3명일 때
친구가 3명일 경우는 아래 그림과 같이 2가지 경우밖에 없습니다.
D(3) = 2
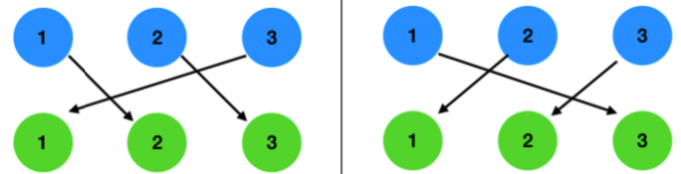
1번 친구가 2의 선물을 선택하고, 2번 친구가 1의 선물을 선택한다면 3번 친구는 3번 선물인 자기 자신의 선물을 선택해야하기 때문에 가능하지 않습니다. 이렇게 3명의 친구로 다른 경우는 나올 수 없습니다.
친구가 4명일 때
이제 친구가 4명일 경우를 생각해 보겠습니다.
경우 1
1의 친구가 2의 선물을 골랐습니다. 그리고 2 역시 1의 선물을 고를 경우 입니다.

이렇게 고르면 3과 4는 2가지 경우의 교란 순열 입니다.
1번 친구가 3번 선물을 고를 수도 있습니다. 마찬가지로 3번 친구도 1번 선물을 고른다면 2, 4는 2가지 경우의 교란 순열 입니다.
4번을 고를 때에도 마찬가지 입니다. 즉 두 사람이 서로 선물을 교환한다면 나머지 사람들로 교란순열을 만들 수 있습니다. 두 사람이 선물을 교환할 경우는 n - 1번 가능 합니다. 위에서도 (2, 1), (3, 1), (4, 1)로 n - 1번 나타납니다. 이것을 식으로 아래와 같이 표현할 수 있습니다.
D1(n) = (n - 1) * D(n - 2)
경우 2
이제 1번과 2번이 선물을 서로 교환하지 않을 경우를 생각해 보겠습니다. 1번 친구가 2번 선물을 골랐다고 해서, 2번 친구가 1번 선물을 고르리라는 보장이 없기 때문 입니다.

1번 친구가 2번 선물을 고르면 이 경우는 2, 3, 4로 이루어진 3개의 교란 순열이라 할 수 있습니다. 경우 1에서는 친구도 3, 4이고, 선물도 3, 4이기 때문에 교란 순열이 이해되지만 이 경우는 친구는 2, 3, 4가 있고 선물을 1, 3, 4가 있기 때문에 교란순열이 아니라 생각할 수도 있습니다.
하지만 잘 생각해보면 친구 2는 선물 1을 고를 수 없습니다. 왜냐하면 친구 2가 선물 1을 고르는 경우는 이미 경우 1에서 모두 고려했기 때문 입니다. 따라서 친구2는 선물 1을 고를 수 없는 것이고, 이로써 3가지의 교란 순열이라 말할 수 있다는 것입니다.
1번 친구가 2번 선물을 고를수도 있고, 3번, 4번도 고를 수 있기 때문에 이것 역시 n - 1번의 경우를 가집니다.
D2(n) = (n - 1) * D(n - 1)
으로 나타낼 수 있습니다.
이제 두 식을 합치면 다음과 같습니다
D(n) = D1(n) + D2(n) = (n - 1)(D(n - 1) + D(n - 2))
따라서 4명의 친구가 선물을 나누는 경우는 다음과 같습니다.
D(4) = 3 * (2 + 1) = 9
4명까지는 9가지라 수형도로 나타낼 수 있습니다.

맨 위가 1, 2, 3, 4가 있고 밑의 9가지가 수형도로 나태낸 교란 순열 입니다.
5명 이상일 때
5명 부터는 수형도로 나타내기에 너무 많습니다.
D(5) = (5 - 1)(D(4) + D(3)) = 4 * (9 + 2) = 44
44가지 경우라 수형도로 나타내기가 힘들어 집니다. 6명일 때는 더욱 위 식이 아니라면 구할 수 없습니다.
교란 순열의 점화식
교란순열은 !n 으로 나타내기도 합니다. 경우의 수를 구하는 n! 의 팩토리얼을 앞에 써준것과 같습니다. 그리고 구하는 공식은 위에서 나타낸 것과 같이 나타낼 수 있습니다.
D(n) = (n - 1)(D(n - 1) + D(n - 2))
이것을 !n으로 표시하면 다음과 같이 됩니다.
!n = (n - 1)(!(n - 1) + !(n - 2))
'알고리즘 설명' 카테고리의 다른 글
| 부동소수점 이해하기 (0) | 2024.04.15 |
|---|---|
| 등차수열과 등비수열 (1) | 2024.03.28 |
| 한 붓 그리기 가능한 경우 (0) | 2024.03.15 |
| 파이썬 음수의 나머지 연산 (0) | 2024.03.11 |
| 2차원 배열 회전하기 (0) | 2024.01.24 |

