목차
2020년 정보올림피아드 1차 필기 시험 초등부 1번부터 5번까지 풀이 진행하겠습니다.
1번

나머지 연산을 이해하는지 묻는 문제 입니다. (A * B) % C 연산은 ((A % C) * (B % C)) % C로 나타낼 수 있습니다.
예를 들어 보겠습니다. (7 * 5) % 3 은 35 % 3 으로 2입니다. 이것을 분배하면 ((7 % 3) * (5 % 3)) % 3으로 (1 * 2) % 3으로 아까와 같이 2가 되는 것을 알 수 있습니다.
3^2020은 2020을 4로 나누면 505가 되고, 3^4를 505번 곱한것과 같습니다. 따라서 이 문제를 풀어보면 다음과 같습니다. ((3^4 % 5) * (3^4 % 5) … (3^4 % 5)) % 5로 나타낼 수 있습니다. 3 ^ 4 % 5는 1이기 때문에 결국 (1 * 1 … * 1) % 5가 됩니다. 1을 505번 곱해도 1이고 5로 나누어주면 1을 가지게 됩니다.
2번

인접 리스트 형태의 자료구조를 “아는 사람”이라는 형태로 표현한 문제 입니다. 위의 예제를 그래프로 표시하면 다음과 같습니다.

위와 같은 그림을 그릴 수 있는지를 묻는 문제 입니다. A가 4명을 안다는 사실은 A와 나머지가 모두 연결되어 있다는 뜻입니다.

A와 나머지의 관계를 위와 같이 표시할 수 있습니다. 다음으로 B는 3명을 알고 있습니다. A와는 이미 연결되어 있기 때문에 가까운 2명과 연결을 하면 3명의 관계를 가질 수 있습니다.

C는 2명을 알고 있고 이미 2명의 연결이 되어 있습니다. 마지막으로 D와 E는 1명을 알 고 있습니다. 위의 그림에서 E의 연결이 2명이기 때문에 잘못 연결 되어 있다는 것을 알 수 있습니다. D와 E의 위치를 바꿔도 마찬가지 입니다. 즉 어떻게 바꿔도 D와 E를 만족시킬 수 없고 결국 이 목록은 만들 수 없다는 것을 알 수 있습니다. 따라서 답은 0이 됩니다.
3번

이기는 경우를 따져보면 쉽게 알 수 있는 문제 입니다. 왼쪽은 이기는 경우, 오른쪽은 지는 경우를 뜻합니다. 이렇게 나타냈을 때 승, 패 정보를 파악해보면 A가 이기는 경우가 몇 가지인지 알 수 있습니다. 경우의 수를 따져보면 아래와 같이 6가지임을 알 수 있습니다.
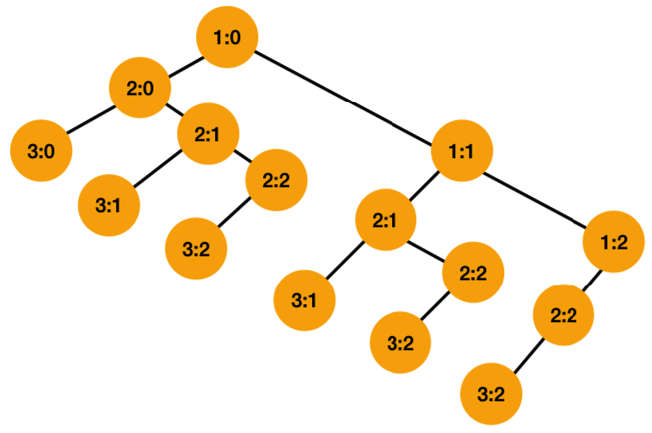
4번

간단한 수학 문제 입니다. 발판이 1초동안 1바퀴 돌 때 손잡이 회전축은 얼마나 도는지 계산하는 문제 입니다. r은 2이고, R은 7이기 때문에 7/2로 3.5초동안 한 바퀴 돌게 됩니다. 총 여섯 바퀴를 돌아야 하기 때문에 3.5 * 6으로 총 21초가 걸리게 됩니다.
5번

왼쪽 상단 ‘나’ 위에 있는 (1, 1)의 위치를 보면 주변에 지뢰가 없습니다. 즉 ‘나’의 위치에는 지뢰가 없다는 것을 알 수 있습니다.

‘나’의 위치 즉 (2, 1)이 0이 됨으로 (2, 2)의 위치에 3이라는 지뢰를 나타내기 위해서는 밑의 3개가 모두 지뢰가 되어야 합니다.

(4, 1)위치의 2는 이미 지뢰를 2개 찾았기 때문에 (5, 1)과 ‘라’위치의 (5, 2)는 지뢰가 없다는 것을 알 수 있습니다.

(4, 2) 위치의 5를 만족하기 위해서는 (4, 3), (5, 3) 모두 지뢰가 있어야 합니다.

(4, 4) 위치의 3이 이미 만족했기 때문에 빈칸으로 남아있는 (4, 4)의 주변이 모두 0이 됩니다.

(3, 5)위치에 0이고, (2, 5)위치에는 1개의 지뢰가 있습니다. 따라서 ‘가’의 위치에 지뢰가 있다는 것을 알 수 있습니다.
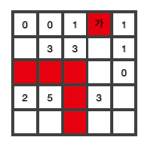
이렇게 ‘가’ 위치가 정답임을 알았습니다. 어렵게 모든 지뢰의 위치를 다 찾아서 문제를 해결했습니다. 하지만 (3, 5)의 위치만 찾아도 문제가 해결 됩니다.

파란색 0을 해결하기 위해 주변의 위치를 전부 지뢰가 없다고 한다면 ‘가’의 위치에 무조건 지뢰가 존재하게 됩니다.
'알고리즘 설명 > 정보올림피아드 필기' 카테고리의 다른 글
| 2020년 정보올림피아드 필기 초등부(11 ~ 2 - 3) (2) | 2024.03.26 |
|---|---|
| 2020년 정보올림피아드 필기 초등부(6 ~ 10) (0) | 2024.03.25 |
| 2019년 정보올림피아드 필기 중등부(2 - 4 ~ 2 - 8) (0) | 2024.03.23 |
| 2019년 정보올림피아드 필기 중등부(11 ~ 2 - 3) (0) | 2024.03.21 |
| 2019년 정보올림피아드 필기 중등부(6 ~ 10) (0) | 2024.03.20 |



