목차
2023년 정보올림피아드 1차대회 초등부 필기 6번부터 10번까지 문제 풀이 입니다.
1번부터 5번은 아래 링크 확인 바랍니다.
2024.04.07 - [알고리즘 설명/정보올림피아드 필기] - 2023년 정보올림피아드 필기 초등부(1 ~ 5)
6번

부분의 개수가 가장 적게 나오기 위해서는 나누는 기준이 길다는 뜻입니다. 따라서 ab나 ba로 최대한 나누는 것이 부분의 개수를 적게 나오게 하는 것입니다. 그리디 형태로 문제를 해결하면 됩니다.
- ba ba b ba ab a
- ba ba b ba a ba
최대한 길이가 길게 만들면서 나누면 위와 같이 두 가지 경우가 나오게 되고 그 경우는 6개의 부분이라는 것을 알 수 있습니다.
7번

교환으로 어떤 수를 만드는 방법은 버블 정렬의 방법과 같습니다. 즉 이 문제는 버블 정렬이 몇 번 일어나는지 묻는 문제이며 그것은 가고자 하는 위치를 몇 번만에 도달할 수 있는지 찾으면 해결 됩니다.

위와 같이 첫 번째 1은 3번 이동해야 하며, 두 번째 1 역시 3번, 세 번째 1은 1칸 이동해야 하므로 총 7번의 교환이 필요합니다.
8번

양말은 총 280짝이 있습니다. 여기서 10켤레의 양말을 얻을 수 있는 최선은 20짝을 집었을 때 모두 짝이 맞는 경우 입니다. 최악의 경우는 20짝을 집었을 때 16짝으로 8켤레가 나오고 나머지는 한짝씩 있는 경우 입니다. 어떤식으로 집어도 양말들의 개수는 280짝으로 충분히 많기 때문에 어느 색깔이 다 소진되는 경우는 없습니다.

만약 파란 양말이 60짝으로 위와 같이 안나왔다고 하고 개수가 더 많은 빨간 양말, 녹색 양말이 하나씩 더 나왔다고 하면 빨간 양말 한짝과 녹색 양말 한짝과 만나 10켤레가 완성이 됩니다. 그래서 결론적으로 최악의 경우가 되는것은 위처럼 8켤레가 완성 되고 빨간색, 녹색, 파란색, 검정색이 각각 하나씩 남는 경우 입니다.
이제 21번째에 아무 색깔이나 상관 없이 나온다면 4개의 남는 짝과 맞게 되어 총 9켤레가 됩니다.

이와 같이 초록색 양말이 하나 추가되어 9 켤레가 되었습니다. 이제 22번째의 최악의 경우는 또 초록색이 나와 짝이 맞지 않는 경우 입니다. 만약 초록색이 아닌 다른색이 나오면 10켤레가 완성이 되게 됩니다.

이제 23번째에 어떤 색깔의 양말이 나와도 10켤레가 완성이 됩니다. 따라서 최악의 경우 10켤레를 얻을 수 있는 경우는 23개의 양말을 고를때 임을 알 수 있습니다.
9번

매 번 콘서트에 꽂혀있는 것을 뽑고 새로운 가전제품을 꽂는다면 14번을 교체해야 합니다. 최대한 교체를 적게해야 합니다. 그러기 위해서는 앞으로 얼마 후에 교체할 수 있는지 알면 좋습니다. 교체해야하는 시기가 먼 것부터 교체한다면 최소로 교체할 수 있습니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 교체횟수 | |
| 처음 | 5 | 12 | 7 | 4 |
1, 2, 3, 4가 콘센트에 꽂혀있고 각각 1은 다음에 사용하기 까지 5번 남았고, 2는 12번, 3은 7번, 4는 4번 남았습니다. 가장 멀게 남은 2부터 교체를 시작합니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 교체 횟수 | |
| 처음 | 5 | 12 | 7 | 4 | |||||
| 5 | 4 | 6 | 3 | 8 | 1 |
2번 콘센트를 빼고 5번을 꽂아주었습니다. 1, 3, 4번 콘센트는 다음 교체까지 각각 1씩 줄어들었습니다. 그리고 5의 콘센트를 다음 사용하는 것이 8번 남은 것을 표시하였습니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 교체 횟수 | |
| 처음 | 5 | 12 | 7 | 4 | |||||
| 5 | 4 | 6 | 3 | 8 | 1 | ||||
| 6 | 3 | 5 | 2 | 4 | 2 |
5번 콘센트가 8번 뒤에나 교체하기 때문에 6번 콘센트로 교체해 줍니다. 다음에는 3번 콘센트가 5번이나 남아있기 때문에 교체를 합니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 교체 횟수 | |
| 처음 | 5 | 12 | 7 | 4 | |||||
| 5 | 4 | 6 | 3 | 8 | 1 | ||||
| 6 | 3 | 5 | 2 | 4 | 2 | ||||
| 7 | 2 | 1 | 3 | 8 | 3 |
1, 4, 6번 콘센트의 횟수가 1씩 줄고, 7번 콘센트는 다음 사용하기까지 8번이 남았습니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 교체 횟수 | |
| 처음 | 5 | 12 | 7 | 4 | |||||
| 5 | 4 | 6 | 3 | 8 | 1 | ||||
| 6 | 3 | 5 | 2 | 4 | 2 | ||||
| 7 | 2 | 1 | 3 | 8 | 3 | ||||
| 4 | 1 | 0 | 2 | 7 | 3 | ||||
| 1 | 8 | 0 | 1 | 6 | 3 | ||||
| 6 | 7 | 0 | 4 | 5 | 3 |
다음 숫자는 4, 1, 6으로 교체가 없어도 사용가능합니다. 콘센트에 그대로 꽂혀있고 숫자만 1씩 줄어 듭니다. 숫자가 0이 안되고 다시 커진 것은 다음에 한 번 더 사용하기 때문에 다시 남은 숫자를 표시해 준 것입니다.
이렇게 남은 숫자가 많은 콘센트만 교체하면 충분히 최소 횟수를 구할 수 있습니다. 더 이상 교체 되지 않는 콘센트는 X로 표시하였습니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 교체 횟수 | |
| 처음 | 5 | 12 | 7 | 4 | |||||
| 5 | 4 | 6 | 3 | 8 | 1 | ||||
| 6 | 3 | 5 | 2 | 4 | 2 | ||||
| 7 | 2 | 1 | 3 | 8 | 3 | ||||
| 4 | 1 | 0 | 2 | 7 | 3 | ||||
| 1 | 8 | 0 | 1 | 6 | 3 | ||||
| 6 | 7 | 0 | 4 | 5 | 3 | ||||
| 3 | 6 | 7 | 3 | 4 | 4 | ||||
| 8 | 5 | 2 | 3 | X | 5 | ||||
| 5 | 4 | X | 1 | 2 | 6 | ||||
| 6 | 3 | X | 0 | 1 | 6 | ||||
| 7 | 2 | X | 0 | 0 | 6 | ||||
| 2 | 1 | X | X | 0 | 7 | ||||
| 1 | 0 | X | X | 0 | 7 | ||||
| 3 | 0 | X | X | X | 8 |
마지막 3번 가전제품까지 사용하면 교체 횟수가 8번이라는 것을 알 수 있습니다.
10번
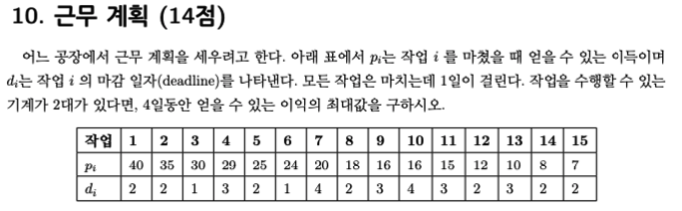
최대 이익을 얻기 위해서 마감일 부터 계산해 봐야 합니다. 앞에서부터 계산하는 것이 아니라 끝에서부터 계산하는 이유는 마감 일자를 넘길 수는 없지만, 미리 끝낼 수는 있기 때문입니다. 마감일에 마치는 것보다 미리 마치는 것이 더 이득이 되는 경우도 있기 때문 입니다.
먼저 4일차부터 생각해 보겠습니다.

4일차는 두개밖에 없기 때문에 무조건 해야합니다. 두개의 작업으로 36의 이익을 얻을 수 있습니다.

3일차 입니다. 가장 이익이 많이 나는 경우는 4일차 29와 9일차 16입니다. 3일차에 45의 이득을 얻을 수 있습니다.

2일차에는 1일에 40, 2일에 35가 가장 큰 이득입니다. 두 날짜의 합은 75 입니다. 3일차중 이미 계산된 4일 9일을 제외하고는 계산에 참여 가능합니다.

1일차 입니다. 3일차에 30과 5일차의 25가 최대값 입니다. 5일차는 2일까지 끝내면 되지만 더 이득이 크기 때문에 1일차에 작업 진행한 것입니다. 따라서 1일차 55를 얻을 수 있습니다.
이제 4일차 36, 3일차 45, 2일차 75, 1일차 55를 모두 더하면 211이 됩니다.
'알고리즘 설명 > 정보올림피아드 필기' 카테고리의 다른 글
| 2023년 정보올림피아드 필기 초등부(16 ~ 20) (0) | 2024.04.10 |
|---|---|
| 2023년 정보올림피아드 필기 초등부(11 ~ 15) (0) | 2024.04.09 |
| 2023년 정보올림피아드 필기 초등부(1 ~ 5) (0) | 2024.04.07 |
| 2022년 정보올림피아드 필기 초등부(16 ~ 20) (0) | 2024.04.06 |
| 2022년 정보올림피아드 필기 초등부(11 ~ 15) (0) | 2024.04.05 |



