목차
2020년 정보올림피아드 1차대회 중등부 필기 6번부터 10번까지 문제풀이 입니다.
이전 문제는 아래 링크 확인 바랍니다.
2024.04.09 - [알고리즘 설명/정보올림피아드 필기] - 2020년 정보올림피아드 필기 중등부(1 ~ 5)
6번
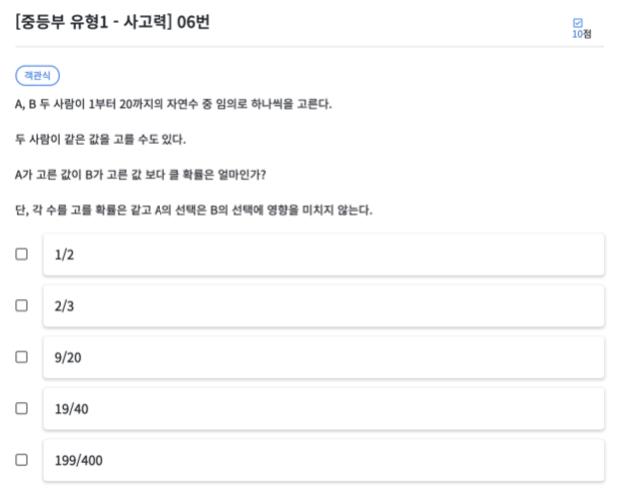
먼저 두 사람이 1부터 20까지의 자연수 중 임의로 하나씩 고를 경우의 수를 알아보겠습니다.
A와 B 모두 20개를 고를 수 있기 때문에 20 * 20으로 400의 경우의 수를 가집니다.
다음으로 A가 B보다 큰 수를 고를 경우의 수 입니다.
B가 1을 선택하면 A는 2부터 20까지중 아무거나 선택했을 때 A가 더 큽니다.
B가 2를 선택했다면 A는 3부터 20까지 고를 수 있습니다.
마지막으로 B가 20을 선택했다면 A는 아무것도 선택할 수 없습니다. 즉 처음에는 19개, 다음에는 18개, 다음에는 17개 이런식으로 0개까지 선택이 가능합니다. A가 선택 가능한 경우는 0부터 19까지의 등차수열의 합과 같습니다.
$$ \frac{n(n+1)}{2}=\frac{19*20}{2}=190 $$
전체 경우의 수가 400이고 A가 이길 경우의 수가 190이기 때문에 전체 확률은 190 / 400으로 19 / 40이 됩니다.
7번
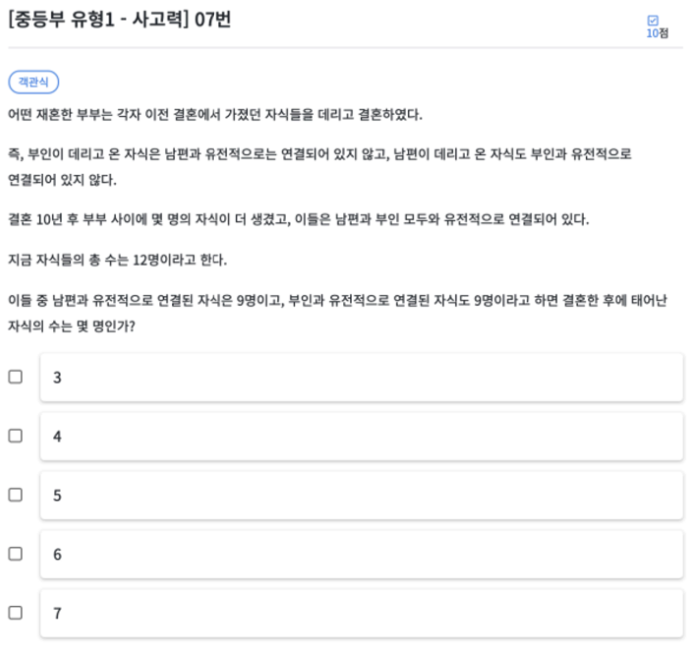
남편이 데리고 온 자식이 x명, 부인이 데리고 온 자식이 y명이라고 하겠습니다. 그리고 같이 낳은 자식이 z라고 한다면 다음의 식이 성립합니다.
x + y + z = 12
x + z = 9, y + z = 9
전체 자식의 수는 12명이니까 남편이 데리고 온 아이와 부인이 데리고 온 아이, 그리고 같이 낳은 아이 전체의 합이 12명 입니다. 다음으로 남편이 유전적으로 연결된 자식은 데리고온 자식 x명과 같이 낳은 자식 z명 입니다. 부인 역시 마찬가지로 y + z가 되는 것입니다.
두 식을 연립해서 풀면 x = 3, y = 3, z = 6이 됩니다. 따라서 결혼 후 태어난 자식은 총 6명이 됩니다.
8번
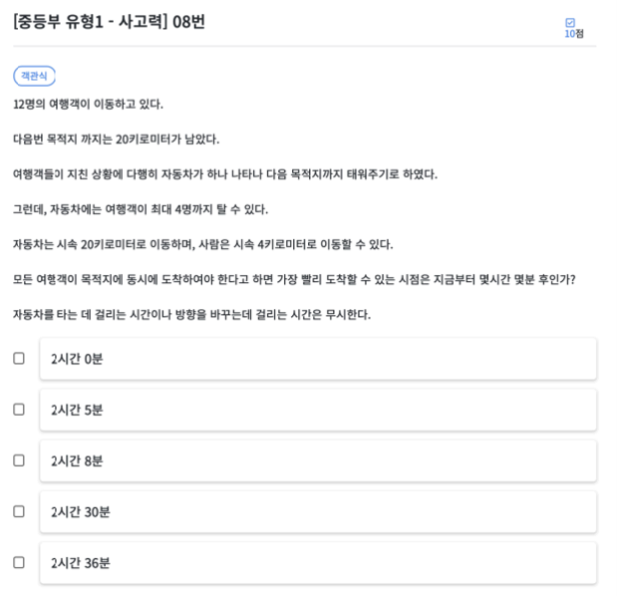
초등부 7번과 같습니다. 7번 확인 바랍니다.
https://davincicoding.tistory.com/122#7%EB%B2%88
2020년 정보올림피아드 필기 초등부(6 ~ 10)
2020년도 정보올림피아드 1차 대회 초등부 필기 6번부터 10번까지 문제 풀이 입니다. 1번부터 5번까지는 아래 링크 확인 바랍니다. 2024.03.24 - [알고리즘 설명] - 2020년 정보올림피아드 필기 초등부(1
davincicoding.co.kr
9번
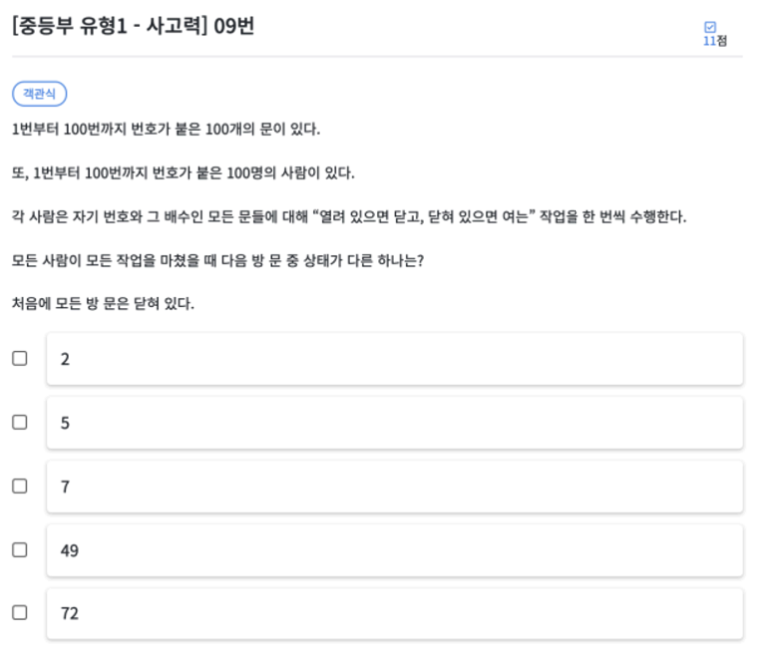
처음에 모든 방 문이 닫혀 있습니다. 1번이 100번까지 모든 문을 열어 놓습니다.
2번은 2의 배수의 문을 모두 닫습니다.
3번은 홀수 문은 모두 닫고, 짝수 문은 열게 됩니다.
이 문제는 에라토스테네스의 채와 비슷한 형태로 진행되는 문제 입니다. 당연하게도 소수와 연관된 문제라는 것을 알 수 있습니다. 소수만 찾는 에라토스테네스의 채가 아니라 한 단계 더 나아가 자신의 약수를 만날 경우 열리거나 닫히거나를 반복 합니다. 2, 5, 7은 소수이기 때문에 열린 문을 한 번 닫으면 다시 열리지 않습니다.
49는 1일 때 열린 것을 7일 때 닫고, 다시 49일 때 열게 됩니다. 그 외에는 열리거나 닫히지 않습니다.
72는 2^3 * 3^2 입니다. 따라서 1일 때 열리고, 2일 때 닫히고, 3일 때 열리고, 4일 때 닫히고 6일 때 열리고, 8일 때 닫히고, 9일 때 열리고, 12일 때 닫히고, 18일 때 열리고, 24일 때 닫히고, 36일 때 열리고, 72일 때 닫힙니다. 어렵게 계산했지만 72의 모든 약수가 홀수면 열리고, 짝수면 닫힌다고 생각하면 좀 더 쉽습니다.
즉 위 문중 49만 열려있고 나머지는 모두 닫혀있다는 것을 알 수 있습니다.
10번

초등부 8번과 같습니다. 링크에서 8번 확인 바랍니다.
https://davincicoding.tistory.com/122#8%EB%B2%88
2020년 정보올림피아드 필기 초등부(6 ~ 10)
2020년도 정보올림피아드 1차 대회 초등부 필기 6번부터 10번까지 문제 풀이 입니다. 1번부터 5번까지는 아래 링크 확인 바랍니다. 2024.03.24 - [알고리즘 설명] - 2020년 정보올림피아드 필기 초등부(1
davincicoding.co.kr
'알고리즘 설명 > 정보올림피아드 필기' 카테고리의 다른 글
| 2020년 정보올림피아드 필기 중등부(2-4 ~ 2-8) (3) | 2024.04.14 |
|---|---|
| 2020년 정보올림피아드 필기 중등부(11 ~ 2 - 3) (0) | 2024.04.13 |
| 2020년 정보올림피아드 필기 중등부(1 ~ 5) (0) | 2024.04.11 |
| 2023년 정보올림피아드 필기 초등부(16 ~ 20) (0) | 2024.04.10 |
| 2023년 정보올림피아드 필기 초등부(11 ~ 15) (0) | 2024.04.09 |



