목차
2022년도 정보올림피아드 1차대회 필기 중등부 6번부터 10번까지 문제 풀이 입니다.
이전 문제는 아래 링크 확인 바랍니다.
2024.04.20 - [알고리즘 설명/정보올림피아드 필기] - 2022년 정보올림피아드 필기 중등부(1 ~ 5)
6번

정육각형에 7개의 점을 놓을 수 있는 방법은 많지만 최대한 멀리 놓을 수 있는 방법은 다음과 같습니다.
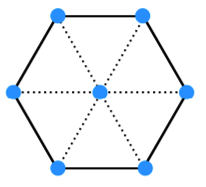
비둘기집 원리에 의해 두 점을 멀리 떨어뜨려 놓아도 나머지 점들과 가까워지기 때문에 적어도 한 쌍의 점은 한 변의 길이인 3이상 떨어지게 만들 수 없습니다.
7번

초등부 10번 문제와 같습니다. 아래 링크를 통해 10번 문제 확인 바랍니다.
https://davincicoding.tistory.com/132#10%EB%B2%88
2022년 정보올림피아드 필기 초등부(6 ~ 10)
2022년도 정보올림피아드 1차대회 필기 초등부 6번부터 10번까지 문제 풀이 입니다. 이전 문제는 아래 링크 확인 바랍니다. 2024.04.03 - [알고리즘 설명] - 2022년 정보올림피아드 필기 초등부(1 ~ 5) 6번
davincicoding.co.kr
8번

7개 이상 연속으로 만들 수 있는 정수의 시작을 찾으면 됩니다.
7개 이상 연속이 되면 모든 금액을 만들 수 있게 됩니다. 예를 들어 a원부터 a + 6원까지 연속으로 만들어져 있다고 생각하겠습니다.
a원에다가 7원을 더하면 a + 7원이 됩니다. a + 1원에 7원을 더하면 a + 8원이 됩니다. 이렇게 a + 6원에다 7원을 더하면 a + 13원이 됩니다. 14원을 더하고 싶다면 7원을 2개 더하면 됩니다. 이렇게 끊임없이 수를 만들 수 있기 때문에 거스름돈의 최소인 7원에 맞춰 7개 연속만 되면 모든 금액을 만들 수 있습니다.
7, 9, 11원은 각각 2원씩 차이가 납니다. 즉 7의 배수에 2를 더한 금액, 4를 더한 금액은 금방 만들 수 있습니다.
만들 수 있는 금액을 생각해 보겠습니다.
7원으로 만들 수 있는 금액은 다음과 같습니다.
7, 14, 21, 28, 35
9원으로 만들 수 있는 금액은 다음과 같습니다.
9, 18, 27, 36, 45
11원으로 만들 수 있는 금액은 다음과 같습니다.
11, 22, 33, 44, 55
만들 수 있는 금액을 하나하나 만들다 보면 연속된 금액을 만들 수 있습니다.
- 9 * 3 = 27
- 7 * 4 = 28
- 11 + 9 * 2 = 29
- 9 + 7 * 3 = 30
- 9 + 11 * 2 = 31
- 7 * 2 + 9 * 2 = 32
- 11 * 3 = 33
이렇게 7개 연속된 숫자를 만들 수 있습니다. 따라서 x의 최솟값은 27 입니다.
9번

이 문제와 똑같은 DP 문제가 있습니다. 아래 문제를 확인해 보면 같은 문제임을 알 수 있습니다.
https://davincicoding.tistory.com/130
[백준 1328] 고층 빌딩
문제 출처 : https://www.acmicpc.net/problem/1328 1328번: 고층 빌딩 상근이가 살고있는 동네에는 빌딩 N개가 한 줄로 세워져 있다. 모든 빌딩의 높이는 1보다 크거나 같고, N보다 작거나 같으며, 같은 높이
davincicoding.co.kr
계산이 복잡한 문제이니 이런 문제는 최대한 나중에 푸는것이 좋습니다. 위 풀이에서 알 수 있는 점화식을 풀어보면 다음과 같은 식이 나옵니다.
dp(6, 3, 2) = dp(5, 2, 2) + dp(5, 3, 1) + dp(5, 3, 2) * (6 - 2)
이것을 계산하면 dp(5, 2, 2)는 22, dp(5, 3, 1)은 11, dp(5, 3, 2)는 18이 나옵니다.
22 + 11 + 18 * 4 = 33 + 72 = 105가 나옵니다.
10번

세 수의 곱이 최대가 되기 위해서는 양수 3개를 곱하던가, 음수 2개, 양수 1개를 곱하면 됩니다. 절대값이 큰 두 음수가 있다면 양수 3개를 곱하는 것보다 크게 만들 수 있습니다.
-6 * 6 * -7 이렇게 세 수를 곱해 252를 얻을 수 있습니다.
'알고리즘 설명 > 정보올림피아드 필기' 카테고리의 다른 글
| 2022년 정보올림피아드 필기 중등부(16 ~ 20) (1) | 2024.04.22 |
|---|---|
| 2022년 정보올림피아드 필기 중등부(11 ~ 15) (0) | 2024.04.22 |
| 2022년 정보올림피아드 필기 중등부(1 ~ 5) (1) | 2024.04.20 |
| 2021년 정보올림피아드 필기 중등부(16 ~ 20) (1) | 2024.04.18 |
| 2021년 정보올림피아드 필기 중등부(11 ~ 15) (0) | 2024.04.17 |



