목차
2020년 정보 올림피아드 2차 대회에서 초등부 2번, 중등부 1번 문제였던 종이접기, 백준 온라인 저지에서 20187번을 풀어 보도록 하겠습니다.
문제 출처 : https://www.acmicpc.net/problem/20187
문제 이해하기
어릴적에 종이를 얼마나 접을 수 있을지 꼬깃꼬깃 접었던 기억이 있습니다. 그렇게 종이를 접고 접다보면 최종적으로 1 X 1 크기의 정사각형이 됩니다. 여기에 4등분 하여 하나의 위치에 구멍을 뚫고 접었던 반대로 풀기 시작하면서 구멍이 뚫린 위치를 출력해주면 됩니다.
마지막 1 X 1 정사각형의 위치는 어떻게 잡으면 될까요? 규칙적으로 접고 접었다가 다시 펼치는 알고리즘을 생각해보면 분할 정복으로 문제를 해결할 수 있습니다. 전체크기를 하나하나 줄여 나가다보면 제일 마지막에 한점으로 만나게 되고 그점에 구멍을 뚫고 다시 펼치면 원래의 종이크기가 될 것이고 어디에 구멍이 뚫려있는지 알 수 있습니다.
코드 작성
말로 설명하기 보다 코드를 보면서 이해하는 것이 빠르기 때문에 코드를 작성하고 이야기를 이어 나가겠습니다.
입력 받기
먼저 입력을 받습니다. 종이의 크기를 나타내는 정수 k 와 접는 순서 folds, 그리고 구멍을 뚫을 위치 h값을 차례대로 입력 받습니다.
k = int(input())
folds = input().split()
h = int(input())
초기화
다음으로 접었다가 펴줄 색종이를 만들어 줍니다. 종이의 한 변의 크기가 2 ** k 이기 때문에 이 길이를 N으로 지정해 두었습니다. 그리고 각 위치는 아직 종이를 뚫지 않았기 때문에 0으로 초기화를 하겠습니다.
N = 2 ** K
pape = [[0] * N for _ in range(N)]
색종이 함수 만들기
색종이를 접어줄 함수를 만들어 보겠습니다. 우리는 상하 방향으로 k번, 좌우 방향으로 k번 색종이를 접습니다. 어느 방향으로 종이를 접을지 모르니 상하에 쓸 인자 fi, 좌우에 쓸 인자 fj로 만들어 주겠습니다. 그리고 종이의 크기를 인자로 주겠습니다. si, sj는 종이의 좌측 상단의 위치 입니다. 그리고 ei, ej는 종이의 우측 하단의 위치 입니다.
def solve(i, j, sy, sx, ey, ex):
pass
solve(0, 0, 0, 0, N, N)색종이 함수의 기본 형태는 위와 같이 만들 수 있습니다. 아직 내용 작성을 하지 않아 pass로 넘겼습니다. 아래에서 함수의 내용을 작성할 예정입니다. solve(0, 0, 0, 0, N, N)을 실행하면 분할정복이 진행하면서 결과를 얻을 수 있습니다. solve 함수에 들어가는 인자들을 살펴보면 아직 접기가 한 번도 실행되지 않았기 때문에 i, j값은 0 입니다. 다음으로 종이가 아직 접혀있지 않기 때문에 종이의 왼쪽 상단의 좌표 sy, sx는 0, 0 입니다. 다음으로 오른쪽 하단의 좌표 ey, ex 는 N, N 이 됩니다.
색종이 접기
이제 folds 값에 따라 종이를 접는 부분을 만들어 보겠습니다.
def solve(i, j, sy, sx, ey, ex):
f = folds[i + j]
if f == 'U': # 상
i += 1
ey = (sy + ey) // 2
solve(i, j, sy, sx, ey, ex)
elif f == 'D': # 하
i += 1
sy = (sy + ey) // 2
solve(i + 1, j, sy, sx, ey, ex)
elif f == 'L': # 좌
j += 1
ex = (sx + ex) // 2
solve(i, j, sy, sx, ey, ex)
else: # 우
j += 1
sx = (sx + ex) // 2
solve(i, j, sy, sx, ey, ex)접는 방법은 folds에 들어 있습니다. i + j 의 인덱스 값을 통해 접는 방법을 확인할 수 있습니다. 접는 방법이 f에 저장되고 이것을 통해 분할정복이 시작 됩니다.
상단으로 접는 U의 경우 시작 좌표는 그대로 이지만 끝 좌표는 반으로 접혀있기 때문에 y의 값이 시작 y와 끝 y의 중간이 됩니다. 그래서 ey의 값은 (sy + ey) // 2 가 됩니다.
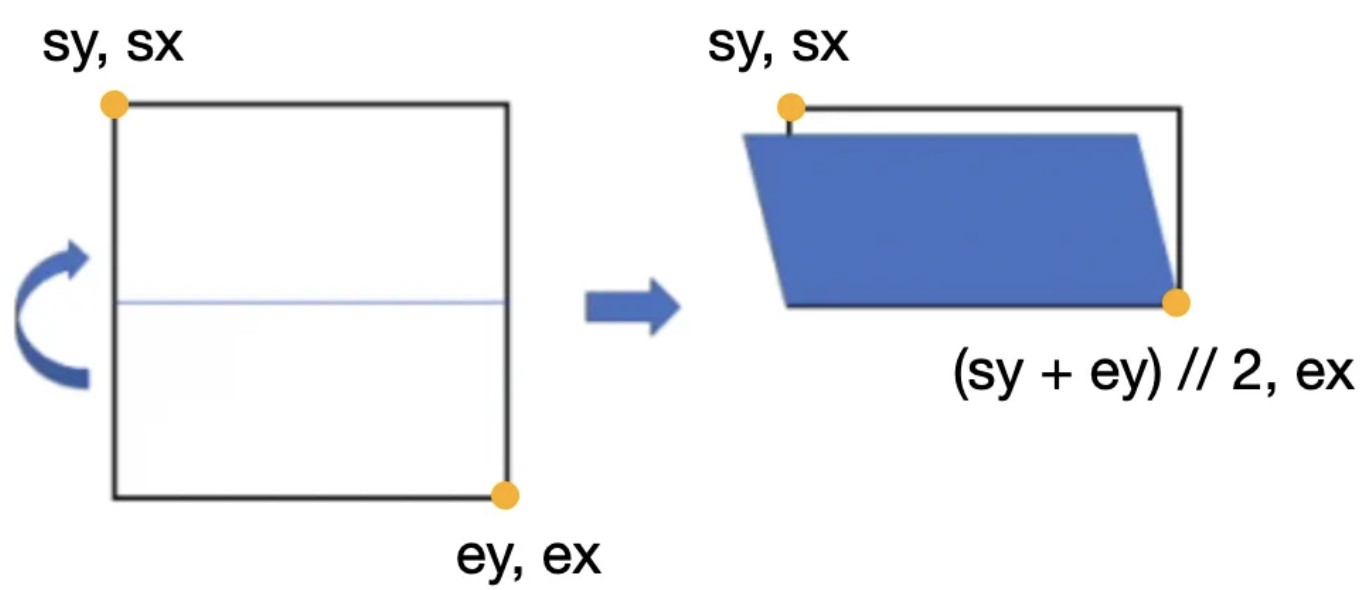
같은 방법으로 D의 경우 밑으로 접혔기 때문에 시작 y의 위치가 중간이 됩니다. L의 경우 왼쪽으로 접었기 때문에 끝 x의 값이 반이 되C고 마지막으로 R의 경우는 오른쪽으로 접혔기 때문에 시작 x의 값이 반이 됩니다.
종료 조건과 구멍 위치
재귀 함수를 사용하면 종료 조건이 필수적으로 있어야 합니다. 그렇지 않으면 무한 루프에 빠지기 때문입니다. 이 문제에서 종료조건은 색종이의 크기가 1 X 1이 될 때 입니다. 이것은 상하로 K번, 좌우로 K번 접었을 때 색종이의 크기가 1이 됩니다. 따라서 i의 값이 k, j의 값이 k가 되면 종료된다고 할 수 있습니다.
def solve(i, j, sy, sx, ey, ex):
if i == k and j == k:
paper[sy][sx] = h
return
solve 함수의 가장 위쪽에 종료조건을 적어줍니다. 접기가 종료되는 2 * k번째가 되었을 때 종이의 위치에 구멍을 뚫어줄 위치 h를 paper 넣어줍니다. paper의 위치는 접고 접어 마지막 sy, sx 값이 됩니다.
종이 펼치기
1 X 1의 크기로 접혀있는 종이를 다시 펼치기 시작하면서 구멍의 위치를 알 수 있습니다. U로 접은 것을 다시 펼치면 아래로 돌아갑니다. 반대로 D로 접은 것은 위로 돌아갑니다. L로 접은 것은 오른쪽이 되고, R인 경우는 왼쪽으로 돌아갑니다. 그럼 구멍의 위치 h는 아래와 같이 됩니다.

가운데 뚫은 구멍 h의 값 0, 1, 2, 3의 위치가 U, D, L, R에 따라 원래의 위치로 돌아갔을 때 어떤 숫자가 되는지 나타낸 것입니다. 접은 것을 펼치기 때문에 아래로 접는 방법인 D가 위에 표시되어 있고, 왼쪽으로 접는 방법 L이 오른쪽에 표시된 것입니다. 그럼 접은 것을 펼쳤을 때 구멍의 위치는 다음과 같이 나타낼 수 있습니다.
df ={
'D' : [2, 3, 0, 1],
'U' : [2, 3, 0, 1],
'R' : [1, 0, 3, 2],
'L' : [1, 0, 3, 2]
}
아래로 접는 D를 펼쳤을 때 0 번째 위치의 구멍은 2번이 되고, 1 번째 위치의 구멍은 3번이 되고, 2 번째 위치의 구멍은 0번이 되고, 3 번째 위치의 구멍은 1이 되는 것입니다.
위로 접은 것 펼치기
U로 입력 받은 경우 위로 접습니다. 이것을 다시 펼치는 경우를 확인해 보겠습니다.
for y in range(2 ** (k - 1 - i)):
for x in range(sx, ex):
paper[ey + y][x] = df[f][paper[ey - y - 1][x]]
첫 번째 for문 부터 알아보겠습니다. 종이를 한 번 접을 때마다 원래 길이의 반 씩 줄어듭니다. 반대로 접은 것을 펼칠 때마다 원래 종이 길이의 두배가 늘어납니다. 예를 들어 k가 4인 경우 종이의 전체 길이는 2 ** 4로 16 입니다. 한 번 접으면 길이가 8이 되고, 또 한 번 접으면 길이는 4가 됩니다. 이것을 수식으로 나타내면 2 ** (k - 1 - i)가 됩니다.
x의 범위는 시작인 sx부터 끝인 ex까지가 범위가 됩니다. 다음으로 paper의 위치에 대해 알아보겠습니다.

U로 접혀있던 종이를 아래로 펼치는 경우는 위의 그림과 같이 표현할 수 있습니다. 거울에 있는 것처럼 구멍의 위치는 반대 방향으로 변경되어 나타납니다. 아래로 펼쳐진 종이의 시작은 ey이고, 원래 종이의 끝은 ey - 1입니다. 아래 부분은 ey에 1씩 늘려나가고, 윗 부분은 ey - 1에 1씩 줄여나가면서 값을 적어나가면 됩니다.
조금 어렵게 느껴질 수 있지만 하나하나 따져나가면서 코드가 어떻게 동작하는지 확인해 보시기 바랍니다.
같은 방식으로 아래로 접은 것을 펼치는 코드, 왼쪽으로 접은 것을 펼치는 코드, 오른쪽으로 접은 것을 펼치는 코드 전체를 확인해 보겠습니다.
if f == 'U':
ey = (sy + ey) // 2
solve(i + 1, j, sy, sx, ey, ex)
for y in range(2 ** (k - i - 1)):
for x in range(sx, ex):
paper[ey + y][x] = df[f][paper[ey - y - 1][x]]
elif f == 'D':
sy = (sy + ey) // 2
solve(i + 1, j, sy, sx, ey, ex)
for y in range(2 ** (k - i - 1)):
for x in range(sx, ex):
paper[sy - y - 1][x] = df[f][paper[sy + y][x]]
elif f == 'L':
ex = (sx + ex) // 2
solve(i, j + 1, sy, sx, ey, ex)
for y in range(sy, ey):
for x in range(2 ** (k - j - 1)):
paper[y][ex + x] = df[f][paper[y][ex - x - 1]]
else:
sx = (sx + ex) // 2
solve(i, j + 1, sy, sx, ey, ex)
for y in range(sy, ey):
for x in range(2 ** (k - j - 1)):
paper[y][sx - x - 1] = df[f][paper[y][sx + x]]
위로 접은 것과 비슷하지만 조금씩 차이가 있습니다. 그림을 그려가며 어느 위치가 펼쳤을 때 어디로 가는지 따져나가면 코드를 이해할 수 있을 것입니다.
전체 코드
그럼 전체 코드를 확인해 보겠습니다.
k = int(input())
folds = input().split()
h = int(input())
N = 2 ** k
paper = [[-1] * N for _ in range(N)]
df ={
'D' : [2, 3, 0, 1],
'U' : [2, 3, 0, 1],
'R' : [1, 0, 3, 2],
'L' : [1, 0, 3, 2]
}
def solve(i, j, sy, sx, ey, ex):
if i == k and j == k:
paper[sy][sx] = h
return
f = folds[i + j]
if f == 'U':
ey = (sy + ey) // 2
solve(i + 1, j, sy, sx, ey, ex)
for y in range(2 ** (k - i - 1)):
for x in range(sx, ex):
paper[ey + y][x] = df[f][paper[ey - y - 1][x]]
elif f == 'D':
sy = (sy + ey) // 2
solve(i + 1, j, sy, sx, ey, ex)
for y in range(2 ** (k - i - 1)):
for x in range(sx, ex):
paper[sy - y - 1][x] = df[f][paper[sy + y][x]]
elif f == 'L':
ex = (sx + ex) // 2
solve(i, j + 1, sy, sx, ey, ex)
for y in range(sy, ey):
for x in range(2 ** (k - j - 1)):
paper[y][ex + x] = df[f][paper[y][ex - x - 1]]
else:
sx = (sx + ex) // 2
solve(i, j + 1, sy, sx, ey, ex)
for y in range(sy, ey):
for x in range(2 ** (k - j - 1)):
paper[y][sx - x - 1] = df[f][paper[y][sx + x]]
solve(0, 0, 0, 0, N, N)
for row in paper:
print(*row)
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 2624] 동전 바꿔주기 (0) | 2024.11.07 |
|---|---|
| [백준 17616] 등수 찾기 (0) | 2024.11.03 |
| [백준 32069] 가로등 (1) | 2024.10.03 |
| [백준 4779] 칸토어 집합 (2) | 2024.10.01 |
| [백준 31963] 두 배 (0) | 2024.09.26 |


