목차
병합 정렬이라고 불리는 머지 소트(Merge Sort)에 대해 알아보겠습니다. 다양한 정렬 알고리즘이 있지만 다빈치코딩 알고리즘에는 이분 정렬에 대해서만 소개했었습니다. 이유는 어짜피 시간복잡도가 비슷하고 이분 탐색만 알아도 정렬에 관한 문제를 푸는데 큰 어려움이 없기 때문입니다.
하지만 Inversion Counting 에 대해 소개하고 세그먼트 트리로 푸는 방법만 알려주고, 정작 Inversion Counting 으로 풀 수 있는 문제 버블 소트를 풀 때에는 Merge sort 로 해결하였던 것이 생각나 merge sort에 대해서도 설명해야 겠다는 생각을 하였습니다.
Merge Sort 란?

위키피디아에 있는 merge sort의 설명 이미지 입니다. 분할 정복과 비슷한 형태로 진행되는 것을 알 수 있습니다. 왜냐하면 merge sort 자체가 분할 정복 알고리즘중의 하나이기 때문 입니다. 그렇기에 분할을 하고 그것을 다시 합쳐주는 과정을 거쳐 정렬이 됩니다.
그림의 [6, 5, 3, 1, 8, 7, 2, 4] 의 숫자로 예를 들어 보겠습니다.
분할 단계
먼저 처음 리스트의 숫자들을 반으로 나누어 줍니다.

[6, 5, 3, 1], [8, 7, 2, 4] 두 개의 리스트로 나누어졌습니다. 재귀 함수를 통해 이 과정을 하나의 요소만 남을 때까지 반복합니다.
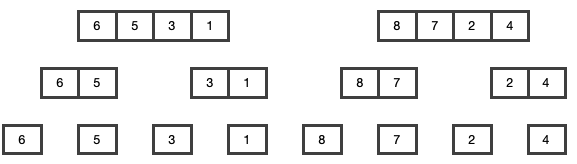
최종적으로 맨 아래와 같이 하나의 요소들만 남았습니다.
정복 단계
분할이 끝나면 이제 다시 합쳐 줍니다. 이 때 정렬을 하면서 합치게 됩니다.
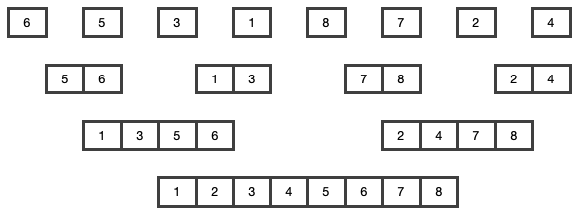
[6], [5]는 정렬이 되어있지 않기 때문에 합쳐주면서 [5, 6]으로 만들어 줍니다. 그럼 [5, 6], [1, 3], [7, 8], [2, 4]로 합쳐지게 됩니다. 이 항목들을 다시 순서대로 합쳐주다보면 결국 맨 아래와 같이 순서대로 정렬되는 것을 알 수 있습니다.
코드로 풀어보기
그럼 이 과정을 코드로 알아보겠습니다.
입력 받기
따로 문제가 있는 것이 아니기 때문에 입력은 위의 리스트 그대로 받겠습니다.
arr = [6, 5, 3, 1, 8, 7, 2, 4]
N = len(arr)
merge_sort(0, N)
print(arr)입력 받은 arr 리스트가 merge_sort를 거쳐 다시 출력되는 형태로 코드를 작성하겠습니다.
분할 단계
def merge_sort(start, end):
if end - start <= 1:
return
mid = (start + end) // 2
merge_sort(start, mid)
merge_sort(mid, end)
merge(start, end)분할 정복과 마찬가지로 계속 반으로 쪼개어 나누어 줍니다. 종료 조건은 end - start 가 1보다 작거나 같은 경우 입니다. 즉 항목이 하나거나 없을 때까지 계속 나누어 줍니다. 다 나누어지면 merge를 통해 다시 합쳐지게 됩니다.
병합 단계
def merge(start, end):
mid = (start + end) // 2
i, j = start, mid
merged_arr = []
while i < mid and j < end:
if arr[i] < arr[j]:
merged_arr.append(arr[i])
i += 1
else:
merged_arr.append(arr[j])
j += 1병합 단계 입니다. 나누어져 있던것을 정렬하여 합쳐줍니다. i가 왼쪽 리스트, j가 오른쪽 리스트라 생각하면 이해가 쉽게 될 것입니다.
[5, 6], [1, 3] 두 리스트를 합쳐주는 단계라 생각해 보겠습니다. 먼저 5와 1을 비교합니다. 더 작은 항목을 merged_arr에 넣게 됩니다. 즉 1이 들어가게 됩니다.
다음으로 왼쪽은 그대로 5와 오른쪽은 1 다음인 3을 비교합니다. 3이 더 작기 때문에 3이 merged_arr에 들어가 [1, 3]이 됩니다.
if i < mid:
merged_arr += arr[i : mid]
if j < end:
merged_arr += arr[j : end]이제 j값이 end 보다 커지기 때문에 while 문을 빠져나옵니다. 왼쪽 리스트와 오른쪽 리스트는 이미 정렬이 된 리스트들이기 때문에 병합을 하면서 남는 항목들은 그냥 이어붙여도 정렬되어 있습니다. 그래서 [1, 3]에 [5, 6]을 붙여 [1, 3, 5, 6]이 되게 됩니다.
for i in range(start, end):
arr[i] = merged_arr[i - start]마지막으로 arr의 값을 변경합니다. 새로운 리스트를 매 번 생성하는 것보다 정렬하고 싶은 리스트를 바로 변경하여 메모리를 절약할 수 있습니다.
전체 코드
전체 코드로 확인해 보겠습니다.
arr = [6, 5, 3, 1, 8, 7, 2, 4]
N = len(arr)
def merge(start, end):
mid = (start + end) // 2
i, j = start, mid
merged_arr = []
while i < mid and j < end:
if arr[i] < arr[j]:
merged_arr.append(arr[i])
i += 1
else:
merged_arr.append(arr[j])
j += 1
if i < mid:
merged_arr += arr[i : mid]
if j < end:
merged_arr += arr[j : end]
for i in range(start, end):
arr[i] = merged_arr[i - start]
def merge_sort(start, end):
if end - start <= 1:
return
mid = (start + end) // 2
merge_sort(start, mid)
merge_sort(mid, end)
merge(start, end)
merge_sort(0, N)
print(arr)Merge Sort에 대해 알아보았습니다. 아래 문제로 Merge sort에 대한 감을 익혀보시기 바랍니다.
'알고리즘 설명' 카테고리의 다른 글
| 파이썬의 문자를 숫자로, 숫자를 문자로 바꾸기 (0) | 2023.11.20 |
|---|---|
| 최소공통조상(LCA) (0) | 2023.10.09 |
| LIS 란? (0) | 2023.09.21 |
| Inversion Counting 알고리즘 (0) | 2023.09.11 |
| 페르마의 소정리 (0) | 2023.08.28 |

