목차
문제 출처 : https://www.acmicpc.net/problem/9465
9465번: 스티커
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 n (1 ≤ n ≤ 100,000)이 주어진다. 다음 두 줄에는 n개의 정수가 주어지며, 각 정수는 그 위치에 해당하는 스티커의
www.acmicpc.net
간단한 DP 문제 입니다. DP에 대해 잘 모른다면 어렵게 느껴질 수 있습니다. 스티커의 품질이 좋지 않기 때문에 어떤 스티커를 떼면 그 스티커의 상, 하, 좌, 우에 있는 스티커는 사용할 수 없습니다. 따라서 왼쪽부터 첫 번째 줄의 스티커를 떼었을 때, 두 번째 줄의 스티커를 떼었을 때, 아무것도 떼지 않았을 때, 이렇게 세가지의 경우를 생각해서 문제를 해결해야 합니다.
문제 이해하기
첫 번째 예제를 함께 해보면서 문제를 이해해 보도록 하겠습니다.

이와 같이 스티커가 있습니다. 첫 번째 열의 윗 줄은 50, 아랫 줄은 30의 점수가 있습니다. 무조건 큰 수인 50을 뜯는 것이 좋은 방법이 아닙니다. 왜냐하면 뒤에 어떤 수가 있어 어느것이 유리해질지 모르기 때문 입니다. 따라서 모든 경우를 다 고려해야 합니다. 윗 줄을 뜯었을 때, 아랫 줄을 뜯었을 때, 뜯지 않았을 때 입니다.

각각 아무것도 뜯지 않은 경우에는 0, 윗 줄을 뜯은 경우 50, 아랫 줄을 뜯은 경우 30의 점수를 얻게 됩니다. 다음으로 두 번째 열을 생각해 보겠습니다.
두 번째 열 아무것도 뜯지 않았다면 첫 번째 열의 최대 점수인 50이 얻을 수 있는 최대 점수 입니다. 윗 줄을 뜯는 다면 첫 번째 열의 윗 줄을 뜯을 수 없습니다.
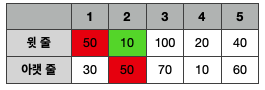
따라서 최대값은 첫 번째 열의 뜯지 않은 경우, 아랫줄을 뜯은 경우의 최대값인 30에 현재 뜯을려고 하는 점수 10을 더해 40이 됩니다.
마지막으로 두 번째 열의 아랫 줄을 뜯는 경우는 첫 번째 열의 윗 줄을 뜯은 경우인 50에 현재 50을 더해 100이 됩니다.

세 번째 열을 계산해 보겠습니다. 아무것도 뜯지 않은 경우는 두 번째 열까지의 최대값 100이 됩니다. 윗 줄을 뜯는 경우는 2번째 아랫줄의 최대 점수 100에 3번 윗 줄을 뜯는 100점을 더해 200점이 됩니다. 아랫줄을 뜯는 경우는 2번째 뜯지 않은 경우 50에 현재 점수 70을 더해 120이 최대 점수가 됩니다.

모든 경우를 다 따져보면 다음과 같은 결과를 얻게 됩니다.

이제 마지막 줄의 결과를 확인하여 최대값인 260을 출력하면 됩니다. 그럼 지금 알아본 것을 직접 코드로 확인해 보겠습니다.
입력 받기
T = int(input())
for _ in range(T):
n = int(input())
arr = [list(map(int, input().split())) for _ in range(2)]
테스트 케이스 T를 입력 받습니다. 다음으로 각 테스트 케이스에 몇 열로 되어 있는지를 나타내는 n을 입력 받습니다. 그리고 2줄로 되어 있는 각각의 스티커 점수들을 입력 받습니다.
최대값 계산하기
왼쪽부터 각각의 줄에서 어떤 스티커를 뜯을지 정해주어야 합니다. 첫 번째 줄의 스티커를 뜯었을 때, 두 번째 줄의 스티커를 뜯었을 때, 스티커를 뜯지 않았을 때 세가지 경우에 대해서 처리를 해주어야 합니다.
dp = [[0] * (n+1) for _ in range(3)]
for i in range(1, n+1):
#뜯지 않았을 때
dp[0][i] = max(dp[0][i-1], dp[1][i-1], dp[2][i-1])
# 1번을 뜯었을 때
dp[1][i] = max(dp[0][i-1], dp[2][i-1]) + arr[0][i-1]
# 2번을 뜯었을 때
dp[2][i] = max(dp[0][i-1], dp[1][i-1]) + arr[1][i-1]dp에는 각 줄에서 얻을 수 있는 점수의 최대값을 넣을 것 입니다. 총 3줄로 0번행에는 아무것도 뜯지 않았을 때의 최대값, 1번행은 윗 줄을 뜯었을 때의 최대값, 2번 행은 아랫 줄을 뜯었을 때의 최대값이 들어가게 됩니다. for문을 통해 각 열에서 어떤 스티커를 뜯었을 때 얻게되는 점수의 최대값을 계산해 줍니다.
뜯지 않았을 때
예를 들어 3번째 줄의 스티커 중 아무것도 뜯지 않았다면, 2번째 까지 얻을 수 있는 최대값을 가져오게 됩니다.
dp[0][i] = max(dp[0][i-1], dp[1][i-1], dp[2][i-1])
윗 줄을 뜯었을 때
예를 들어 3번째 윗 줄을 뜯는다고 한다면, 윗 줄 2번째 스티커는 뜯을 수 없습니다. 왜냐하면 스티커를 뜯게되면 그 스티커의 상, 하, 좌, 우는 뜯을 수 없기 때문입니다. 따라서 2번째줄을 하나도 뜯지 않은 0번의 점수와, 아랫줄의 점수중 최대값을 얻게 됩니다. 여기에 방금 뜯은 3번째 윗 줄의 스티커 점수를 더해줍니다.
dp[1][i] = max(dp[0][i-1], dp[2][i-1]) + arr[0][i-1]
아랫줄을 뜯었을 때
예를 들어 3번째 아랫줄의 스티커를 뜯게 된다면 2번째 아래줄의 스티커는 뜯을 수 없습니다. 따라서 2번째 줄까지 아무것도 뜯지 않은 경우의 점수와, 윗줄을 뜯었을 때의 점수의 최대값에 3번째 아랫줄의 스티커의 값을 더해 값을 구해 줍니다.
dp[2][i] = max(dp[0][i-1], dp[1][i-1]) + arr[1][i-1]
결과 출력하기
ans = max(dp[0][n], dp[1][n], dp[2][n])
print(ans)
마지막줄을 뜯었을 때, 윗 줄을 뜯었을 때, 아랫 줄을 뜯었을 때 세 가지 경우 중 가장 큰 값을 출력해주면 됩니다.
전체 코드 보기
그럼 전체 코드를 확인해 보도록 하겠습니다.
T = int(input())
for _ in range(T):
n = int(input())
stk = [list(map(int, input().split())) for _ in range(2)]
dp = [[0] * (n+1) for _ in range(3)]
for i in range(n):
# 똗지 않았을 때
dp[0][i+1] = max(dp[0][i], dp[1][i], dp[2][i])
# 1번을 뜯었을 때
dp[1][i+1] = max(dp[0][i], dp[2][i]) + stk[0][i]
# 2번을 뜯었을 때
dp[2][i+1] = max(dp[0][i], dp[1][i]) + stk[1][i]
ans = max(dp[0][n], dp[1][n], dp[2][n])
print(ans)'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 25405] 2022년 정보 올림피아드 2차 "레벨 업" (2) | 2023.10.11 |
|---|---|
| [백준 11437] LCA (1) | 2023.10.10 |
| [백준 1976] 여행 가자 (1) | 2023.10.04 |
| [백준 15686] 치킨 배달 (0) | 2023.09.27 |
| [백준 12015] 가장 긴 증가하는 부분 수열 2 (0) | 2023.09.20 |
