목차
문제 출처 : 쉬운 계단 수
10844번: 쉬운 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
숫자가 계단수인지 아닌지 확인하며 개수를 센다면 시간초과가 발생할 수밖에 없습니다. 이런 문제를 만나면 직접 경우의 수를 따져보며 문제를 어떻게 풀어야 할지 고민하는게 좋습니다.
예제 입력 확인해보기
예제 입력을 보면 1을 입력 하였을 때 9가 출력 됩니다. 0으로 시작하는 수는 계단수가 아니기 때문에 1부터 9까지의 숫자 아무거나 계단수가 됩니다. 따라서 9가 되는 것입니다.
다음으로 2를 입력하면 17이 됩니다. 왜 17이 되는지 따라가보면 앞서 1을 입력한 숫자들이 계단수가 되기 위해 어떻게 바뀌는지 생각하면 알 수 있습니다. 1은 10이나 12가 됩니다. 7은 76이나 78이 됩니다. 즉 한자리였던 숫자가 2자리가 되면서 경우의 수가 2배가 됩니다. 하지만 마지막 숫자인 9는 98만 됩니다. 그렇기에 총 2자리의 계단수는 1부터 8까지 숫자들이 2배가 되고, 9만 98이 되어 총 17개가 됩니다.
3자리수 이상이 되면 앞서 계산한 것과 마찬가지로 2배씩 늘어납니다. 3자리 숫자도 마찬가지로 89는 898만 될 수 있습니다. 또 10이였던 숫자는 101만 가능합니다. 이런식으로 경우의 수를 계산하면 모든 경우의 수를 확인할 수 있습니다.
DP로 해결하기
즉 이 문제는 각각의 숫자들이 있을 때 하나의 자리수가 늘어나면 1부터 8까지는 위에서 추가되거나, 아래에서 추가 됩니다.
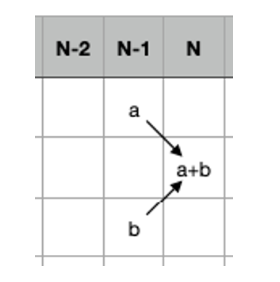
이 그림과 같이 N - 1 번째 a의 경우의 수와 b의 경우의 수의 합인 N번째 a + b가 N번째로 끝나는 수의 경우의 수가 되는 것입니다. 이렇게 경우의 수를 위와 아래에서 더해주면 되지만 마지막 값이 0이거나 9일 경우에는 아래와 같이 한가지 경우만 가능합니다.

0은 더 밑으로 갈 수 없고, 9는 더 위로 갈 수 없기 때문 입니다. 이처럼 0과 9, 그리고 나머지 숫자들의 경우의 수를 DP를 통해 구해줄 수 있습니다.
코드 확인 하기
코드를 통해 알아보도록 하겠습니다.
입력 받기
N = int(input())
MOD = 1_000_000_000
dp = [[0] * 10 for _ in range(N + 1)]
길이가 N인 숫자를 계산하기 위해 N을 입력 받습니다. 다음으로 1,000,000,000으로 나눈 나머지를 출력하기 위해 MOD 값을 세팅합니다. 마지막으로 각각의 숫자의 경우의 수를 계산하기 위해 dp 배열을 만들어 0으로 초기화 하였습니다. dp는 2차 배열로 앞의 숫자는 자리수를 뜻하고 뒤의 숫자는 마지막 숫자가 무엇인지 뜻합니다. 따라서 dp[5][7] 이라고 되어 있으면 5자리 숫자들 중 7로 끝나는 계단수의 개수가 들어 있는 것입니다.
N이 1일 경우
for i in range(1, 10):
dp[1][i] = 1
N이 1인 경우는 1부터 9까지의 숫자 하나만 존재하기 때문에 이들의 경우의 수가 9개 입니다. N이 1인 경우 0은 포함되지 않기 때문에 포함하지 않았습니다.
N이 2 이상인 경우
for i in range(2, N + 1):
dp[i][0] = dp[i - 1][1]
dp[i][9] = dp[i - 1][8]
for j in range(1, 8 + 1):
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1]
dp[i][j] %= MOD
N이 2보다 큰 경우 입니다. 위에서 언급했듯이 0, 9인 경우와 그외를 계산해 주어야 합니다. 끝자리가 0인 경우는 i - 1번째 숫자가 1일 경우 입니다. 마찬가지로 끝자리가 9인 경우는 i - 1번째 숫자가 8인 경우 입니다.
그 외인 1부터 8까지는 i - 1 번째 숫자가 바로 위의 숫자와 바로 아래의 숫자가 됩니다. 그리고 마지막으로 MOD 값으로 나누어주어 숫자가 무한정 커지는 것을 막아줍니다.
경우의 수 구하기
total = 0
for i in range(10):
total += dp[N][i]
total %= MOD
print(total)
최종 경우의 수를 구하기 위해서는 마지막 N번째 자리의 0부터 9까지의 경우의 수를 모두 더해주면 됩니다. 숫자가 너무 커지는 것을 막기 위해 MOD값으로 나누어 주었습니다. 최종적으로 total을 출력해 줍니다.
전체 코드
N = int(input())
MOD = 1_000_000_000
dp = [[0] * 10 for _ in range(N + 1)]
for i in range(1, 10):
dp[1][i] = 1
for i in range(2, N + 1):
dp[i][0] = dp[i - 1][1]
dp[i][9] = dp[i - 1][8]
for j in range(1, 8 + 1):
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1]
dp[i][j] %= MOD
total = 0
for i in range(10):
total += dp[N][i]
total %= MOD
print(total)
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 28217] 2023 정올 1차 두 정삼각형 (0) | 2024.01.25 |
|---|---|
| [백준 11779] 최소 비용 구하기 2 (3) | 2024.01.23 |
| [백준 13308] 2016 정올 고등부 "주유소" (1) | 2024.01.21 |
| [백준 1219] 오민식의 고민 (1) | 2024.01.01 |
| [백준 1865] 웜홀 - 플로이드 워셜 풀이 (1) | 2023.12.17 |


