목차
다빈치코딩 알고리즘에 나머지 정리에 대해 설명하다 분배 법칙에 대해 글을 쓰다보니 나눗셈에 대해서는 왜 분배 법칙이 적용이 안되는지를 설명하게 되었습니다. 그러면서 페르마의 소정리를 이용하면 나눗셈도 나머지 연산을 할 수 있다고 하였는데 그것에 대해 설명하려 합니다. 다빈치코딩 알고리즘은 초등학교 고학년에서 중학교 저학년 친구들을 대상으로 하였기 때문에 페르마의 소정리를 다루는 것은 책이 아닌 블로그에 정리하는 것이 맞다고 느껴졌습니다.
페르마의 소정리(Fermat’s little theorem)
페르마의 소정리는 다음과 같이 정의 됩니다. “소수 p와 p의 배수가 아닌 정수 a가 있을 때 a^p를 p로 나눈 나머지와 a를 p로 나눈 나머지는 같다” 입니다. 수학적으로는 아래와 같이 표현 합니다.
$$ a^p \equiv a \pmod p $$
코딩을 하는 입장에서 위와 같은 수식보다는 a^p % p = a % p 가 훨씬 이해하기 쉽게 느껴지기 때문에 이렇게 표현 하였습니다.
코딩에서 응용
그럼 이것으로 코딩에서 나머지 연산의 분배 법칙을 어떻게 적용할까요? 위의 식의 양 변을 a로 나누어 줍니다. 그럼 아래와 같은 식이 됩니다.
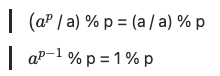
1을 p로 나누어도 결국 1이기 때문에 다음과 같이 됩니다.
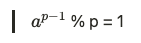
여기에 a를 한 번 더 양변에 나누어 줍니다.

여기까지 이해되면 완료된 것입니다. 즉 위의 어떤 수 나누기 a 를 어떤 수 곱하기 $a^{p-2}$ 로 나타낼 수 있다는 뜻 입니다. 나누기가 곱하기로 바뀌었기 때문에 나머지 연산의 분배 법칙이 사용 가능하고 아래와 같은 식으로 나타낼 수 있습니다.
(B / A) % p = (B * A^(p - 2)) % p = (B % p) * (A^(p - 2) % p ) % p
페르마의 소정리 증명
사용 방법과 코딩에서 어떻게 사용하는지 알게 되었으니 이것이 왜 이렇게 되는지 증명을 해보겠습니다. 아래 내용이 이해가 안된다면 굳이 증명까지는 몰라도 됩니다.
1부터 p-1
p는 소수라고 하였습니다. 소수는 1과 자기 자신외에는 나누어지지 않습니다. 따라서 1부터 p - 1까지의 숫자가 있다면 이 숫자들은 p로 나누어도 나누어지지 않기 때문에 자신의 수 그대로 됩니다. 예를 들어 p가 소수 7이라면 1부터 6까지의 숫자를 7로 나누어도 자기 자신이 되어 나머지가 같은 숫자가 없습니다.
a, 2a, .. (p-1)a
위에서 구한 숫자들에 임의의 수 a를 곱하면 a, 2a, 3a, … (p-1)a가 됩니다. 이 숫자들을 p로 나누게 되면 나머지도 모두 다른 수가 됩니다.
1부터 p-1까지 p로 나눈 나머지가 모두 다르다는 것은 쉽게 이해되지만, a, 2a, 3a, … (p-1)a를 p로 나눈 나머지가 모두 다른 수가 된다는 것은 쉽게 이해되지 않습니다. 이것을 증명하기 위해서 나머지가 같은 두 수가 있다고 가정해보면 됩니다.
p로 나누었을 때 나머지가 같은 서로 다른 두 수 b * a, c * a 가 있다고 하겠습니다. 그럼 b * a, c * a를 아래와 같이 표현할 수 있습니다.
b * a = p * i + r
c * a = p * j + r
두 식을 빼주면 다음과 같은 식이 나옵니다.
(b - c) * a = (i - j) * p
이 식이 만족하려면 a가 p의 배수 이여야 합니다. 하지만 처음 페르마의 소정리를 설명할 때 a는 p의 배수가 아니라고 하였기 때문에 만족하지 않습니다. 따라서 (b - c)와 (i - j)가 0이 되어야 합니다. 그래야 a가 p의 배수가 아니더라도 위 식을 만족합니다. 하지만 우리가 b, c를 선택할 때 서로 다른 두 수라고 하였습니다. 따라서 이것도 만족하지 않습니다. 이렇게 모순이 발생함으로 위 식에서 나머지가 같은 두 수가 없다는 것을 알수 있습니다.
결론
1부터 p-1까지 수들과, a부터 (p-1)a 까지 수들은 p로 나눈 나머지들이 1대 1 매칭이 된다는 뜻입니다. 이것이 왜 중요할까요? 두 식을 모두 곱해보면 답이 나옵니다.
두 식 곱하기
1 * 2 * 3 … * (p - 1) 를 p로 나눈 나머지와 a * 2a * 3a * … * (p-1)a를 p로 나눈 나머지는 같습니다. 이것을 식으로 표현하면 다음과 같이 됩니다.
$$ (p - 1) ! \equiv (p - 1)! \times a^{p-1} \pmod p $$
1부터 (p-1)까지 곱한 값은 (p-1)!가 되고, 1a, 2a, … (p-1)a 까지 곱한것은 a가 p-1개 있으므로 $a^{p-1}$ 가 되고, 앞의 숫자들이 (p-1)!이 됩니다. 양변을 (p-1)!로 나누어주면 다음과 같이 됩니다.
$$ 1 \equiv a^{p-1} \pmod p $$
양변의 위치를 바꿔주면
$$ a^{p-1} \equiv 1 \pmod p $$
가 되고, 양 변에 a를 곱해주면 페르마의 소정리의 공식과 같게 됩니다.
$$ a^{p} \equiv a \pmod p $$
문제 풀기
페르마의 소정리에 대해 알아보았으니 관련 문제를 풀어보도록 하겠습니다. 관련 문제는 다음 포스팅에 이어 작성하겠습니다.
'알고리즘 설명' 카테고리의 다른 글
| 파이썬의 문자를 숫자로, 숫자를 문자로 바꾸기 (0) | 2023.11.20 |
|---|---|
| 최소공통조상(LCA) (0) | 2023.10.09 |
| [알고리즘]Merge Sort (2) | 2023.09.26 |
| LIS 란? (0) | 2023.09.21 |
| Inversion Counting 알고리즘 (0) | 2023.09.11 |


