목차
2023년도 정보올림피아드 1차대회 필기 중등부 6번부터 10번까지 문제 풀이 입니다.
이전 문제는 아래 링크 확인 바랍니다.
2024.04.23 - [분류 전체보기] - 2023년 정보올림피아드 필기 중등부(1 ~ 5)
2023년 정보올림피아드 필기 중등부(1 ~ 5)
2023년도 정보올림피아드 1차대회 필기 중등부 1번부터 5번까지 문제 풀이 입니다. 1번 초등부 2번과 같은 문제 입니다. 아래 링크를 통해 2번 확인 바랍니다. https://davincicoding.tistory.com/135#2%EB%B2%88 2
davincicoding.co.kr
6번

먼저 3의 배수 혹은 4의 배수는 몇개인지 알아보겠습니다.
3의 배수는 2001 / 3으로 667개 있습니다.
4의 배수는 2001 / 4로 500개 있습니다.
이 값은 3의 배수이면서 4의 배수인 개수도 포함된 것으로 3 * 4 인 12의 배수의 숫자를 빼주어야 합니다.
12의 배수는 2001 / 12 는 166개 입니다.
667 + 500 - 166 = 1001개 입니다.
다음으로 5의 배수가 아닌 수를 구하기 위해서 5의 배수를 빼주어야 합니다.
3의 배수이면서 5의 배수인 15의 배수를 고하고, 4의 배수이면서 5의 배수인 20의 배수를 구하고, 15와 20의 배수와 겹치는 부분인 60의 배수를 빼주어야 합니다.
15의 배수는 2001 / 15 는 133개 입니다.
20의 배수는 2001 / 20 은 100개 입니다.
60의 배수는 2001 / 60 은 33개 입니다.
따라서 위에 1001개중 5의 배수들은 133 + 100 - 33으로 200개로 801개가 5의 배수가 아닙니다.
7번
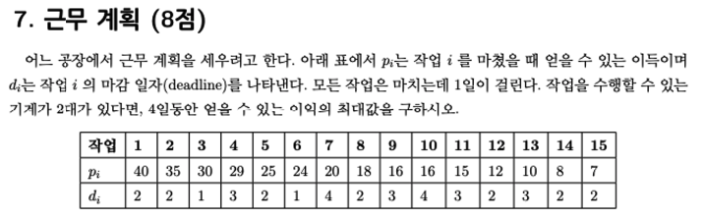
초등부 10번과 같습니다. 아래 링크를 통해 10번 확인 바랍니다.
https://davincicoding.tistory.com/136#10%EB%B2%88
2023년 정보올림피아드 필기 초등부(6 ~ 10)
2023년 정보올림피아드 1차대회 초등부 필기 6번부터 10번까지 문제 풀이 입니다. 1번부터 5번은 아래 링크 확인 바랍니다. 2024.04.07 - [알고리즘 설명/정보올림피아드 필기] - 2023년 정보올림피아드
davincicoding.co.kr
8번

비둘기집 원리로 풀 수 있는 문제 입니다. 먼저 최대한 멀리 4개의 점을 놓아보겠습니다.
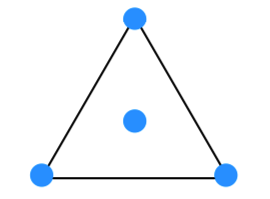
정삼각형의 각 꼭지점에 점을 놓고, 정삼각형의 가운데에 점을 놓습니다. 이렇게 4개의 점을 놓은 후 하나의 점을 최대한 멀리 놓아도 꼭지점에서 중앙에 위치한 점까지의 거리보다 멀어질 수는 없습니다.
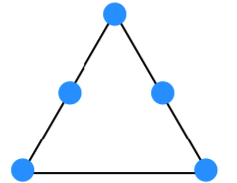
5개의 점을 최대한 멀리 놓으면 위와 같습니다. 변의 길이가 2이기 때문에 각 점까지의 거리는 1입니다. 중간점 끼리의 거리 역시 닮음으로 거리가 1입니다. 따라서 정답은 2번 1.0 입니다.
9번

A가 건달이라면 거짓말을 말해야 하기 때문에 자신을 신사라고 말할 것이고, 신사라고 하더라도 진실을 말하기 때문에 자신이 신사라고 말할 것입니다. 즉 A는 무조건 자신을 신사라고 말할 것입니다.
따라서 B가 A는 자신이 건달이라고 말했다고 한 것은 B가 건달이기 때문에 거짓을 말한 것입니다. C는 거짓을 말한 B에 대해 진실을 말했기 때문에 신사 입니다.
즉 A는 건달인지 신사인지 알 수 없지만 B는 건달, C는 신사 입니다.
10번

초등부 12번과 같습니다. 아래 링크를 통해 12번 확인 바랍니다.
https://davincicoding.tistory.com/137#google_vignette
2023년 정보올림피아드 필기 초등부(11 ~ 15)
2023년 정보올림피아드 1차대회 초등부 필기 11번부터 15번까지 문제 풀이 입니다. 1번부터 10번은 아래 링크 확인 바랍니다. 2024.04.07 - [알고리즘 설명/정보올림피아드 필기] - 2023년 정보올림피아
davincicoding.co.kr
'알고리즘 설명 > 정보올림피아드 필기' 카테고리의 다른 글
| 2023년 정보올림피아드 필기 중등부(16 ~ 20) (2) | 2024.04.26 |
|---|---|
| 2023년 정보올림피아드 필기 중등부(11 ~ 15) (1) | 2024.04.25 |
| 2023년 정보올림피아드 필기 중등부(1 ~ 5) (0) | 2024.04.23 |
| 2022년 정보올림피아드 필기 중등부(16 ~ 20) (1) | 2024.04.22 |
| 2022년 정보올림피아드 필기 중등부(11 ~ 15) (0) | 2024.04.22 |



