목차
2023년도 정보올림피아드 1차대회 필기 중등부 6번부터 10번까지 문제 풀이 입니다.
이전 문제는 아래 링크 확인 바랍니다.
2024.04.23 - [분류 전체보기] - 2023년 정보올림피아드 필기 중등부(1 ~ 5)
2024.04.23 - [분류 전체보기] - 2023년 정보올림피아드 필기 중등부(6 ~ 10)
11번
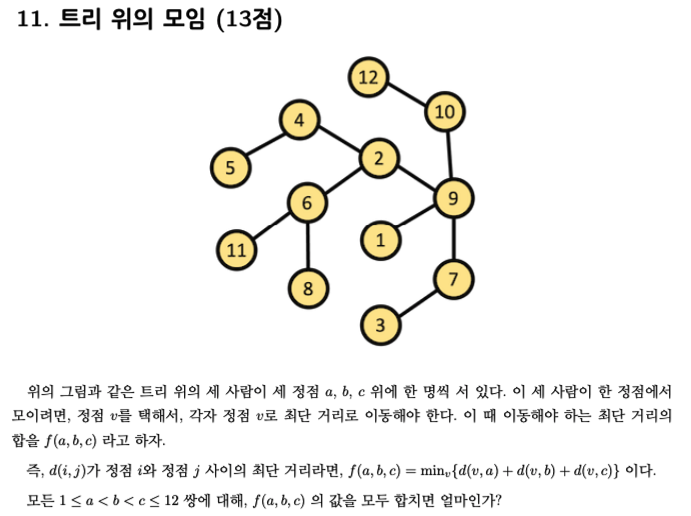
세 개의 점을 찍고 각각의 간선들이 몇 번 사용 되었나 묻는 문제 입니다. 총 12개의 정점이 있고, 여기서 세 개의 점을 고르기 때문에 총 220의 경우의 수를 가집니다.
$$ _{12}C_3 = \frac{12 * 11 * 10}{3 * 2 * 1} = 220 $$
220개의 경우에서 각각의 간선들이 사용 되었는지를 따지는 것입니다.

그림과 같이 빨간색 간선이 사용되었는지를 알기 위해서는 전체 220번의 경우의 수 중에서 12번 정점을 사용하지 않는 모든 경우 입니다. 12번 정점을 사용하지 않는 경우를 계산해 보겠습니다. 12번을 제외한 11개의 정점에서 3개의 정점을 고르는 문제가 됩니다.
$$ _{11}C_3 = \frac{11 * 10 * 9}{3 * 2 * 1} = 165 $$
220 - 165 = 55로 빨간색 정점을 사용하는 경우는 55번 입니다.

이렇게 하나의 간선만 있는 것이 아니라 전체 모양에서 이런 간선이 총 6개가 있어 55 * 6 을 계산하면 총 330이 됩니다.
다음으로 두번째에 위치한 간선을 생각해 보겠습니다.
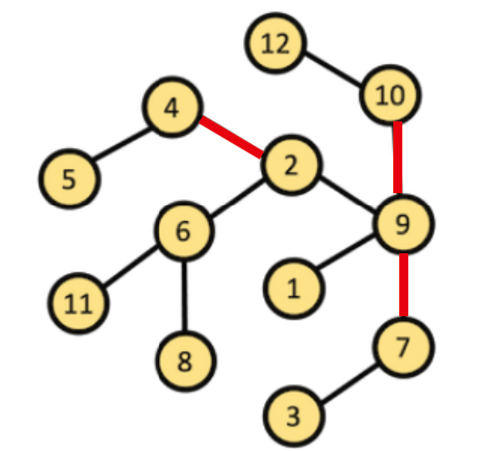
2 - 6 으로 연결된 간선은 2번째에 위치하긴 했지만 경우가 다르기 때문에 따로 계산하겠습니다. 10 - 9로 연결된 간선을 계산해보고 경우가 3가지가 있으니 3배를 하면 됩니다. 총 220개의 경우에서 10, 12번을 제외한 10개의 정점에서 3개의 정점을 고르는 경우를 계산하면 됩니다. 계산해보면 총 120가지가 나오고 220 - 120을 하면 100번 사용된다는 것을 알 수 있습니다. 총 3가지 경우이기 때문에 300번이 됩니다.
마지막 두가지 경우를 생각해 보겠습니다.

먼저 2 - 9의 경우 입니다. 총 220의 경우의 수 중에서 왼쪽 2, 4, 5, 6, 8, 11의 정점만 사용하는 경우는 6C3으로 20가지 입니다. 반대인 1, 3, 7, 9, 10, 12만 사용한 경우 역시 20가지 입니다. 220의 경우 중 왼쪽 20, 오른쪽 20을 뺀 180의 경우에서 2 - 9 간선을 사용 합니다.
다음으로 2 - 6의 간선을 생각해 보겠습니다. 220의 경우에서 11, 6, 8을 뺀 나머지가 9C3 으로 84 입니다. 그리고 6, 8, 11의 경우를 생각해보면 220 - 84 - 1 로 135번의 경우의 수를 가집니다.
이제 모든 숫자를 구했기 때문에 다 더해주겠습니다. 지금까지 구했던 모든 숫자를 더해줍니다.
330 + 300 + 180 + 135 = 945
이렇게 계산하여 정답은 945가 됩니다.
비슷한 문제로 https://davincicoding.tistory.com/11 를 확인할 수 있습니다.
12번

청강생 3명은 자신의 시험지를 채점할 수 있지만 수강생 4명은 자신의 시험지를 채점할 수 없습니다. 수강생만 놓고 생각하면 이것은 바로 교란 순열 문제 입니다. 교란 순열에 대해 알고 있기 때문에 교란 순열의 공식을 대입하여 문제를 해결해 보겠습니다.
교란 순열에 대해서는 아래 링크를 확인해 보시기 바랍니다.
https://davincicoding.tistory.com/119
교란 순열이란?
완전 순열(Complete permutation) 또는 교란(derangement) 순열이라 불리는 순열에 대해 알아보겠습니다. 교란 순열의 예를 들어 보겠습니다. 교란 순열이란? 졸업을 맞이하여 서로를 축하하기 위해 친구 N
davincicoding.co.kr
청강생 3명이 자신의 시험지를 볼 때
먼저 청강생 3명 모두가 자신의 시험지를 채점한다고 생각해 보겠습니다. 그럼 수강생 4명은 모두 자신의 시험지를 채점하면 안됩니다. 교란순열 D4를 구하는 문제로 총 9가지 경우가 있습니다.
청강생 2명이 자신의 시험지를 볼 때
이제 청강생 2명이 자신의 시험지를 채점한다고 생각해 보겠습니다. 수강생 4명, 청강생 1명이 자신의 시험지를 채점하지 않으면 됩니다.
$$ D_n = (n - 1)(D_{n-1} + D_{n - 2}) $$
교란순열 공식은 위와 같습니다. 알려준 교란순열은 다음과 같습니다.
D(1) = 0, D(2) = 1, D(3) = 2, D(4) = 9
위 공식으로 다음 교란 순열을 구해보겠습니다.
D(5) = (5 - 1)(D(4) + D(3)) = 4 * (9 + 2) = 44
44의 경우의 수가 나왔지만 우리는 청강생 2명이 누구인지 모릅니다. 3명중 2명을 고를 경우는 3가지가 있기 때문에 44 * 3으로 132의 경우가 나옵니다.
청강생 1명이 자신의 시험지를 볼 때
청강생 1명만 자신의 시험지를 채점한다면 수강생 4명, 청강생 2명으로 총 6명의 교란 순열 입니다.
D(6) = 5 * (44 + 9) = 265
우리는 청강생 1명이 누군지 모르기 때문에 3가지 경우를 생각해야 합니다. 265 * 3 = 795 가지 경우가 됩니다.
청강생 모두 자신의 시험지를 보지 않을 때
마지막으로 청강생 모두가 자신의 시험지를 보지 않을 경우 입니다. 총 7명의 교란순열을 구해주면 됩니다.
D(7) = 6 * (265 + 44) = 1854
모든 합
이제 모든 경우의 수를 합해주겠습니다.
1854 + 795 + 132 + 9 = 2790
모든 경우의 수는 2790 입니다.
13번

초등부 14번과 같은 문제 입니다. 아래 링크를 통해 14번 확인 바랍니다.
https://davincicoding.tistory.com/137#14%EB%B2%88
2023년 정보올림피아드 필기 초등부(11 ~ 15)
2023년 정보올림피아드 1차대회 초등부 필기 11번부터 15번까지 문제 풀이 입니다. 1번부터 10번은 아래 링크 확인 바랍니다. 2024.04.07 - [알고리즘 설명/정보올림피아드 필기] - 2023년 정보올림피아
davincicoding.co.kr
14번

초등부 17번과 같은 문제 입니다. 아래 링크를 통해 17번 확인 바랍니다.
https://davincicoding.tistory.com/138#17%EB%B2%88
2023년 정보올림피아드 필기 초등부(16 ~ 20)
2023년 정보올림피아드 1차대회 초등부 필기 16번부터 20번까지 문제 풀이 입니다. 1번부터 15번은 아래 링크 확인 바랍니다. 2024.04.07 - [알고리즘 설명/정보올림피아드 필기] - 2023년 정보올림피아
davincicoding.co.kr
15번

초등부 18번과 같습니다. 아래 링크를 통해 18번 확인 바랍니다.
https://davincicoding.tistory.com/138#18%EB%B2%88
2023년 정보올림피아드 필기 초등부(16 ~ 20)
2023년 정보올림피아드 1차대회 초등부 필기 16번부터 20번까지 문제 풀이 입니다. 1번부터 15번은 아래 링크 확인 바랍니다. 2024.04.07 - [알고리즘 설명/정보올림피아드 필기] - 2023년 정보올림피아
davincicoding.co.kr
'알고리즘 설명 > 정보올림피아드 필기' 카테고리의 다른 글
| 2024년 정보올림피아드 필기 초등부(1 ~ 5) (0) | 2025.03.17 |
|---|---|
| 2023년 정보올림피아드 필기 중등부(16 ~ 20) (2) | 2024.04.26 |
| 2023년 정보올림피아드 필기 중등부(6 ~ 10) (0) | 2024.04.24 |
| 2023년 정보올림피아드 필기 중등부(1 ~ 5) (0) | 2024.04.23 |
| 2022년 정보올림피아드 필기 중등부(16 ~ 20) (1) | 2024.04.22 |



