목차
Maximum Subarray(10211)
문제 출처 : https://www.acmicpc.net/problem/10211
1차원 배열에서 가장 큰 부분 배열을 찾는 문제 입니다. 백준 10211번이 대표적인 문제라 할 수 있습니다.
브루트 포스(Brute Force)
이 문제의 가장 쉬운 해결 방법은 브루트 포스로 해결하는 것입니다. 말 그대로 하나하나 다 해보는 것입니다.
입력 받기
T = int(input())
for _ in range(T):
N = int(input())
arr = list(map(int, input().split()))
print(solve())
테스트 케이스 T를 입력 받습니다. 그리고 T개의 배열 정보를 입력 받습니다. N은 배열의 크기이며 arr에 배열 정보를 입력 받습니다. solve 함수를 실행하여 결과를 리턴하고 그 값을 출력합니다.문제 해결하기
브루트 포스 풀이
def solve():
rst = -float("inf")
for i in range(N):
for j in range(i + 1, N + 1):
temp = sum(arr[i:j])
rst = max(rst, temp)
return rst
solve 함수의 코드 입니다. rst는 Maximum Subarray 값을 저장할 변수 입니다. 초기값은 마이너스 무한대로 하여 줍니다.
반복문을 잘 보면 i는 범위가 N인데 j는 i + 1, N + 1 입니다. 이는 리스트의 슬라이싱 때문입니다. 시작값은 포함되지만 끝값은 포함되지 않는 리스트의 슬라이싱의 특징으로 인해 범위에 차이가 있습니다. 슬라이싱에 대해 잘 모른다면 아래 링크를 통해 확인하시기 바랍니다.
https://wikidocs.net/192334#1-
01. 리스트 기본 사용방법
[TOC] # 리스트(list) 리스트는 말 그대로 목록이라는 뜻입니다. 우리가 음악을 들을 때 좋아하는 음악을 모아놓은 플레이 리스트가 있고, 죽기 전에 해보고 싶은 일들을 …
wikidocs.net
두 개의 반복문을 사용하여 i, j 라는 두 지점을 만들었고, 그 지점 사이에 있는 모든 값을 더해 값을 비교하는 방식입니다. 이 코드는 반복문 두 개만 사용한 코드 같지만 사실 sum이라는 함수 역시도 반복문과 똑같습니다. 즉 이 코드는 반복문을 3개 쓰는 것과 똑같다고 할 수 있습니다.
누적합 풀이
sum을 사용하는 부분을 누적합으로 바꿔준다면 반복문을 두 번만 사용해서 문제를 해결할 수 있습니다.
def solve():
ps = [0]
temp = 0
for a in arr:
temp += a
ps.append(temp)
rst = -float("INF")
for i in range(1, N + 1):
for j in range(i, N + 1):
tmp = ps[j] - ps[i - 1]
rst = max(rst, tmp)
return rst
ps는 누적합의 배열입니다. 맨 앞에 0을 넣어주어 1부터 값이 시작하도록 하였습니다. 이는 누적합을 구할 때 0번째 인덱스를 신경 안쓰기 위해서 입니다. 누적합을 만들어주고 밑에서 범위의 합을 구할 때 i의 값이 1부터 시작하는 것을 알 수 있습니다. i - 1 의 값이 0이 되었을 때 누적합의 0번째 값 0을 사용하게 됩니다.
DP 풀이
누적합으로 바꿔 해결을 했지만 좀 더 생각해보면 투 포인터 방식처럼 양쪽에 포인터를 두면 반복문을 하나만 써도 풀이가 가능해 보입니다. 하지만 막상 투 포인터 방식을 사용하려면 왼쪽 포인터를 언제 움직여야할지 애매합니다. 잘 생각해보면 합계의 최대값을 계속 저장하다가 합계가 현재의 숫자보다 작다면 더 이상 해당 합계를 사용하지 않으면 됩니다.
가령 다음과 같은 숫자가 있다고 해보겠습니다.
- 2, 1, -4, 3, 5, -6, 1, 7, -2, 1
2, 1, -4까지의 합은 -1 입니다. 다음 3을 더했을 때 합계는 2로 3만 사용하는 것이 더 이득입니다.

그럼 이제 3부터 다시 합계를 계산해 보겠습니다.
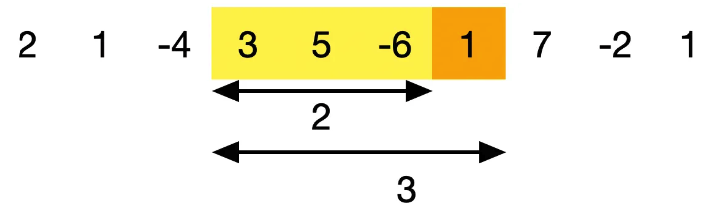
3, 5, -6을 더하면 2로 다음 1을 더했을 때 3이 되어 계속 합계를 유지하는 것이 더 이득이 됩니다.
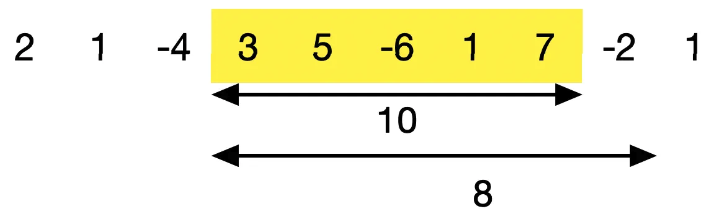
7까지 더하면 10이 되고, -2를 더하면 8이 되어 7까지만 더하는 것이 더 이득이 됩니다. 따라서 답은 3, 5, -6, 1, 7을 더한 10이 됩니다. 그럼 코드를 작성해 보겠습니다.
def solve():
rst = arr[0]
dp = [0] * N
dp[0] = arr[0]
for i in range(1, N):
dp[i] = max(dp[i - 1] + arr[i], arr[i])
rst = max(rst, dp[i])
return rst
Kadane’s 알고리즘
카데인 알고리즘은 위의 DP 방식을 조금 변형한 것입니다. 기존에 dp 배열에 누적된 최대 합계를 저장하는데 dp 배열의 이전 값들을 기억할 필요가 없기 때문에 그냥 변수 하나로 가져가는 방식입니다.
def solve():
rst = arr[0]
curr_total = arr[0]
for i in range(1, N):
curr_total = max(curr_total + arr[i], arr[i])
rst = max(rst, curr_total)
return rst
분할 정복 방식 1
이 문제를 분할 정복 방식으로 풀 수도 있습니다. 사실 분할 정복으로 푸는 것보다는 위의 DP나 카데인 알고리즘이 더 빠르긴 합니다. 다만 이런 방식이 있다는 것을 알고 있다면 나중에 다른 문제 푸는데 도움이 됩니다. 추후 공부 할 세그먼트 트리에서 이 방식을 사용할 예정이기 때문에 미리 알아두는 것입니다.
분할 정복 방식은 작은 문제로 쪼갠 다음 문제를 해결하고 다시 큰 문제로 이어 붙이는 방법입니다. 그래서 우리는 아래와 같이 작은 문제로 쪼갠다음 문제를 해결할 것입니다.

위 그림과 같이 left와 right로 반으로 분할하였습니다. 각각 왼쪽과 오른쪽의 최대값을 구한 다음 두 값 중 큰 값을 고르면 됩니다. 하지만 중요한 부분이 빠져있습니다. 바로 왼쪽과 오른쪽이 모두 포함된 경우가 있기 때문 입니다.

빨간선을 기준으로 나눈 left, right 와 중간지점을 포함한 center까지 총 세 구간의 최대값을 계산해 나갑니다.
def solve(start, end):
if start == end:
return arr[start]
mid = (start + end) // 2
left = solve(start, mid)
right = solve(mid + 1, end)
center = solve_center(start, mid, end)
return max(left, right, center)
이전까지는 solve 함수에 인자가 없었지만 이제 start와 end가 생겼습니다. 마찬가지로 print 해주는 부분도 수정해 주어야 합니다.
for _ in range(T):
N = int(input())
arr = list(map(int, input().split()))
print(solve(0, N - 1))
solve 함수 안에 시작 값인 0과 끝 값인 N - 1을 넣었습니다. 이제 중간의 최대값을 구할 solve_center를 구현하겠습니다.
INF = float("INF")
def solve_center(start, mid, end):
total = 0
left = -INF
for i in range(mid, start - 1, -1):
total = total + arr[i]
left = max(left, total)
total = 0
right = -INF
for i in range(mid + 1, end + 1):
total = total + arr[i]
right = max(right, total)
return left + right
mid부터 시작해서 왼쪽으로 반복문을 진행하면서 left 의 max값을 구하고, 오른쪽으로 진행하면서 right 의max값을 구합니다. 두 값을 더한 값을 리턴해 줍니다.
이렇게 분할정복으로 문제를 해결해 보았습니다. 근데 코드가 조금 마음에 들지 않습니다. 분할 정복을 통해 왼쪽과 오른쪽 값을 구하는 것은 문제가 없지만 가운데 값을 구하기 위해 매 번 반복문을 사용해 반복하고 있습니다. 이 부분을 조금 더 고쳐보도록 하겠습니다.
분할 정복 풀이 2
위 분할 정복 풀이에서 left_max와 right_max 값을 매 번 계산하는 것이 아니라 리턴 해서 사용한다면 반복문 계산을 하지 않아도 될 것 입니다.
solve 함수를 통해 4가지의 값을 매 번 리턴하도록 합니다. 4가지 항목의 값은 다음과 같습니다.
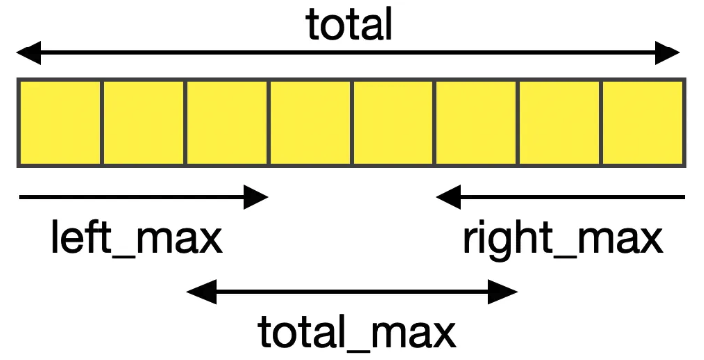
total은 배열 전체의 합계를 뜻합니다. left_max는 배열의 왼쪽에서 시작해서 가지는 최대값 입니다. right_max는 배열의 오른쪽에서 시작해서 가지는 최대값입니다. 마지막으로 total_max는 배열이 가지는 subarray의 최대값 입니다. 우리가 구하려고 하는 maximum subarray 값이 바로 total_max 값 입니다.
먼저 첫 번째 값인 total 즉 전체의 합계를 구하는 방법을 생각해 보겠습니다. 왼쪽을 left, 오른쪽을 right 그리고 그 둘을 합친 것을 my_total 줄여서 mt라고 하겠습니다. mt의 total은 왼쪽의 total과 오른쪽의 total의 합계 입니다. total은 단순 합계를 뜻하기 때문에 크게 어려움 없이 이해가 가능합니다.
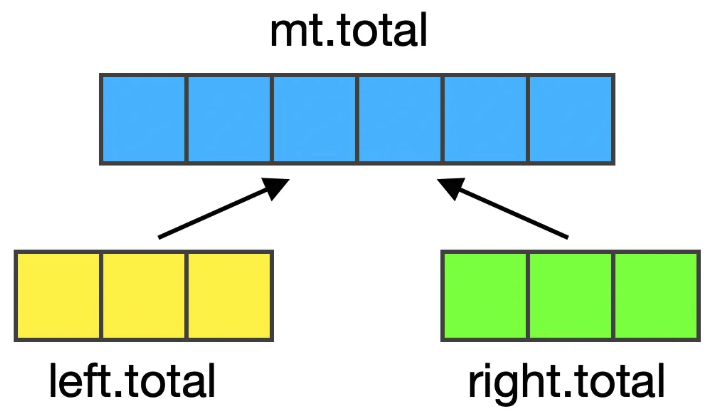
다음으로 left_max 값을 생각해 보겠습니다. left_max란 왼쪽 끝에서 시작해서 합계가 최대값이 되는 구간 입니다. 왼쪽 끝에서 시작한 최대값은 아래 두 가지 종류 중 하나 입니다.
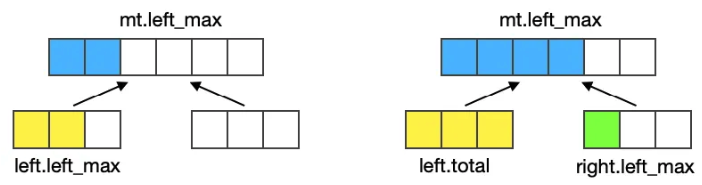
왼쪽의 최대값이 최대인 경우와 왼쪽의 전체와 오른쪽의 left_max가 합친 경우 중 더 큰 값 입니다.
right_max는 left_max와 반대로 구하면 됩니다.

오른쪽의 right_max 값과 오른쪽 total에 왼쪽의 right_max를 합친 값 중 더 큰 값이 right_max가 됩니다.
이렇게 구한 값을 통해 우리가 구하려고 했던 maximum subarray 값인 total_max를 구할 수 있습니다.

total_max 값은 위에서 풀었던 분할 정복1의 방식과 같습니다. 왼쪽의 최대값 혹은 오른쪽의 최대값 그리고 가운데의 최대값 세 개의 값중 최대값이 total_max가 되는 것입니다. 가운데 값인 total_max 값을 분할 정복 1에서는 반복문을 사용해 계산했지만 여기서는 left의 right_max값과 right의 left_max 값의 합으로 바로 구할 수 있습니다. 그럼 코드로 알아보겠습니다.
class MyTotal:
def __init__(self, n = 0):
self.total = n
self.left_max = n
self.right_max = n
self.total_max = n
먼저 MyTotal 클래스 입니다. 해당 클래스에는 4개의 값이 들어갑니다. 전체 합계인 total, 왼쪽 끝값부터 계산한 최대값 left_max, 오른쪽 끝값부터 계산한 최대값 right_max, 그리고 이 maximun subarray 값인 total_max 입니다.
초기값은 0이지만 만약 입력 n이 들어오면 해당 값이 됩니다. 하나의 값이 있는데 그 값의 total, left_max, right_max, total_max 모두 그 하나의 값이 되기 때문 입니다.
def solve(start, end):
if start == end:
return MyTotal(arr[start])
mid = (start + end) // 2
left = solve(start, mid)
right = solve(mid + 1, end)
mt = MyTotal()
mt.total = left.total + right.total
mt.left_max = max(left.left_max, left.total + right.left_max)
mt.right_max = max(right.right_max, right.total + left.right_max)
mt.total_max = max(left.total_max, right.total_max, left.right_max + right.left_max)
return mt
solve 함수 입니다. start와 end가 같아지면 해당 배열 위치의 값을 가지는 MyTotal을 리턴합니다. 그리고 left와 right의 값을 통하여 계산합니다. 계산 내용은 위에서 설명했기 때문에 따로 설명하지 않겠습니다.
최종적으로 solve 함수로 구한 값의 total_max를 출력하면 됩니다.
for _ in range(T):
N = int(input())
arr = list(map(int, input().split()))
print(solve(0, N - 1).total_max)
이렇게 Maximum Subarray 의 다양한 풀이 방법을 알아보았습니다.
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 31965] 회의 장소 (1) | 2025.06.24 |
|---|---|
| [백준 7573] 고기잡이 (2) | 2025.01.27 |
| [백준 1149] RGB 거리 (0) | 2024.12.07 |
| [백준 24552] 올바른 괄호 (4) | 2024.11.27 |
| [백준 2504] 괄호의 값 (1) | 2024.11.26 |

