목차
회의 장소
이 문제는 2024년 정보올림피아드 1차 대회 중등부 2번 문제 입니다.
문제 출처 : https://www.acmicpc.net/problem/31965
문제 이해하기
이 문제는 회의 세트를 통해서 최소 비용을 구하는 문제 입니다. 문제가 복잡해 보이지만 하나하나 이해하면 그렇게 어려운 문제는 아닙니다.
여기서 말하는 비용이란 집에서부터 회의 장소까지 오는 거리와 같습니다.
다음으로 생각할 것은 회의 세트 입니다. 회의 세트는 범위를 이야기 해주고 그 범위 안에 있는 집들을 이야기 합니다. 예제를 보면 회의 세트의 L과 R은 각각 3과 11 입니다. 이 말은 3번과 11번 사이에 있는 3번, 10번, 11번 집이 회의에 참석한다는 뜻입니다.
다음으로 피로도를 구하는 방법을 알아보겠습니다.
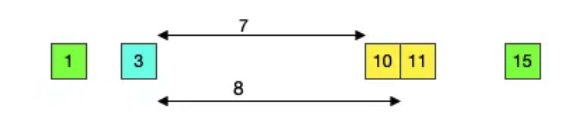
예제를 보면 3번 집에서 회의를 하는 경우 3번은 자신의 집에서 회의를 하기 때문에 피로도가 0 입니다. 그리고 10번과 11번 집에서는 3번과의 거리를 계산하여 7 + 8로 총 15가 됩니다.

회의가 10번에서 진행하는 경우 10번의 피로도는 0이고, 3에서는 7, 11에서는 1입니다. 전체 피로도는 7 + 1로 8이 됩니다.

마지막으로 11번에서 회의를 진행하는 경우 3번에서의 거리는 8, 10번에서의 거리는 1, 11번 자신은 0이 되어 전체 피로도는 8 + 1로 9가 됩니다.
각각의 피로도는 구했고, 이제 회의 세트의 피로도를 구해야 합니다. 회의 세트의 피로도는 인접한 두 집의 회의 비용의 차이의 합으로 정의한다고 합니다. 문제에서는 3 → 11 → 10으로 회의를 진행할 때 |15 - 9| + |9 - 8| = 7로 7이 피로도가 최소라고 합니다. 이 때 모든 경로를 다 뒤져봐야 하기 때문에 실제로는 아래의 경우를 다 따져보아야 합니다.
- 3 → 10 → 11
- 3 → 11 → 10
- 10 → 3 → 11
- 10 → 11 → 3
- 11 → 3 → 10
- 11 → 10 → 3
이 6가지의 경우에서 피로도가 최소가 되는 경우가 3 → 11 → 10으로 회의할 때가 됩니다.
코드 작성
먼저 문제를 풀어보고 복잡도를 줄여나가면서 정답에 다가서도록 하겠습니다. 만약 어떻게 해야할지 아이디어가 금방 떠오른다면 그대로 진행해도 되지만 아이디어가 잘 떠오르지 않는다면 함께 한단계씩 진행해 보겠습니다.
입력 받기
import sys
input = sys.stdin.readline
mii = lambda : map(int, input().split())
N, Q = mii()
X = list(mii())
for _ in range(Q):
L, R = mii()
마을의 집의 수 N과 회의 세트의 수 Q를 입력 받습니다. 다음으로 마을 사람들이 살고 있는 좌표 X를 입력 받습니다. 마지막으로 회의 세트 Q만큼 회의 세트의 정보 L과 R을 입력 받습니다.
이분 탐색
L과 R의 값은 X 좌표의 인덱스 값이 아닙니다. 우리가 알고 있는 사실은 L과 R의 값일 뿐 입니다. 따라서 X 좌표에서 L과 R의 인덱스 값을 찾아야 합니다. 다행히 X는 오름차순으로 정렬되어 있기 때문에 이분 탐색을 통해 쉽게 두 값을 찾을 수 있습니다. L 보다 큰 첫 번째 인덱스 값은 bisect_left를 사용하고 R 보다 작은 마지막 인덱스 값은 bisect_right 값을 사용합니다. bisect_left와 bisect_right의 차이점에 대해 잘 모른다면 아래 링크를 통해 확인 바랍니다.
https://wikidocs.net/206313#bisect
05. 이분 탐색
[TOC] # 이분 탐색(Binary Search) 이분 탐색(Binary Search)은 정렬된 리스트에서 특정 값이 있는지 찾을 때 사용됩니다. 찾는 방법은 다음과 같습니…
wikidocs.net
for _ in range(Q):
L, R = mii()
lo = bisect_left(X, L)
hi = bisect_right(X, R)
if hi <= lo:
print(0)
continue
L보다 큰 첫 번째 인덱스 값은 lo에 들어가고, R보다 작은 마지막 인덱스 값은 hi에 들어갑니다. 엄밀히 말하면 hi에는 R보다 작은 마지막 인덱스 + 1 값이 들어갑니다. hi를 범위로 사용할 것이기 때문에 굳이 정확한 인덱스 위치를 위해 - 1을 할 필요가 없습니다.
각 집의 피로도 구하기
def get_stress(lo, hi, n):
total = 0
for x in X[lo:hi]:
total += abs(n - x)
return total
for _ in range(Q):
L, R = mii()
lo = bisect_left(X, L)
hi = bisect_right(X, R)
if hi <= lo:
print(0)
continue
stress = []
for x in X[lo:hi]:
stress.append(get_stress(lo, hi, x))
회의 세트의 범위는 X[lo:hi] 입니다. hi는 인덱스 + 1한 위치이기 때문에 마지막 값이 안들어가는거 아닌지 걱정하지 않아도 됩니다. x집에서 회의를 진행할 때 get_stress 라는 함수를 통해 피로도를 구해줍니다. 피로도는 회의 세트 전체를 돌면서 각각의 집에서 x까지의 차의 절대값으로 구해줍니다. 이렇게 stress라는 리스트 안에 각집에서의 피로도를 모두 구해줍니다.
최소 피로도 구하기
최소 피로도를 구하기 위해서는 각 집의 순서를 바꿔가면서 최소 피로도를 구해주어야 합니다.
from itertools import permutations
rst = float("INF")
for pl in permutations(stress, len(stress)):
ans = 0
for i in range(1, len(pl)):
ans += abs(pl[i - 1] - pl[i])
rst = min(rst, ans)
print(rst)
permutations는 순열을 구하기 위해서 사용 하였습니다. 순열에 대해 잘 모른다면 아래 링크를 통해 순열에 대해 확인 바랍니다.
https://wikidocs.net/206248#permutation
05. 브루트 포스
[TOC] 브루트 포스(Brute Force)는 알고리즘이라기 보다는 모든 경우를 다 따지며 해를 찾는 방식 입니다. 그럼에도 중요한 이유는 문제를 풀 때 매번 문제에 맞는 알…
wikidocs.net
5개의 집이 있다면 5개의 순서를 어떻게 바꾸느냐에 따라서 최소 피로도가 달라집니다. 따라서 모든 순열을 구해 그 순열에 따라 ans 값을 구해줍니다. 모든 경우에 최소 피로도는 rst에 저장 됩니다.
전체 코드
이렇게 작성한 코드 입니다. 이 코드를 제출하면 5점을 맞을 수 있습니다.
from bisect import bisect_left, bisect_right
from itertools import permutations
import sys
input = sys.stdin.readline
mii = lambda : map(int, input().split())
N, Q = mii()
X = list(mii())
def get_stress(lo, hi, n):
total = 0
for x in X[lo:hi]:
total += abs(n - x)
return total
for _ in range(Q):
L, R = mii()
lo = bisect_left(X, L)
hi = bisect_right(X, R)
if hi <= lo:
print(0)
continue
stress = []
for x in X[lo:hi]:
stress.append(get_stress(lo, hi, x))
rst = float("INF")
for pl in permutations(stress, len(stress)):
ans = 0
for i in range(1, len(pl)):
ans += abs(pl[i - 1] - pl[i])
rst = min(rst, ans)
print(rst)
5점짜리라는 것은 지금까지 우리가 구현한 코드가 맞는 방향이라는 뜻입니다. 범위가 N이 5보다 작을 때, Q가 5보다 작을 때는 정상적으로 동작하지만 N과 Q가 커지면 시간초과가 발생한다는 것입니다. 이제 하나 하나 변경해 나가며 100점을 향해 나아가 보겠습니다.
최적화 해보기
위 코드에서 수 많은 반복문이 있다는 것을 알 수 있습니다. 줄일 수 있는 부분을 생각해 보겠습니다.
회의 세트 피로도 줄이기 1
첫 번째로 회의 세트의 피로도를 줄이는 것입니다. 회의 비용이 감소하거나 증가하는 방향으로 회의를 정렬할 때 피로도가 최소가 됩니다. 예를 들어 회의 피로도가 47, 41, 33, 39, 48 이라고 하겠습니다. 이는 두 번째 예제 (1, 3, 11, 17, 20)의 각 집의 피로도를 구한 것과 같습니다.
이 집들의 피로도를 (48, 47, 41, 39, 33) 으로 정렬했을 때 최소 피로도가 됩니다. 이 상태의 피로도를 계산해 보겠습니다.
|48 - 47| + |47 - 41| + |41 - 39| + |39 - 33| = 1 + 6 + 2 + 6 = 15
이 식을 잘 보면 중간에 47, 41, 39 세 개의 값은 삭제가 됩니다. 즉 다음과 같이 나타낼 수 있습니다.
48 - (47 - 47) - (41 - 41) - (39 - 39) - 33 = 48 - 0 - 0 - 0 - 33 = 15
즉 피로도의 최대값과 최소값만 안다면 회의 세트 전체의 최소 피로도를 계산할 수 있습니다.
max_stress = 0
min_stress = float("INF")
for x in X[lo:hi]:
stress = get_stress(lo, hi, x)
max_stress = max(max_stress, stress)
min_stress = min(min_stress, stress)
print(max_stress - min_stress)
이제 최대 피로도와 최소 피로도를 찾아서 두 값의 차로 작성하였습니다. 순열을 사용하던 것보다는 빠르게 동작이 가능합니다. 이렇게 변경하면 35점을 얻을 수 있습니다.
회의 세트 피로도 줄이기 2
한 번 더 생각을 해보겠습니다. 회의 세트의 전체를 돌면서 각각의 피로도를 구했는데 꼭 그래야 할까요? 잘 생각해보면 가장 피로도가 높은 경우는 양 끝에 있는 경우이고, 가장 피로도가 적은 경우는 가운데 있는 경우 입니다. 위에서 구한 두 번째 예제의 피로도를 확인해 보겠습니다. (47, 41, 33, 39, 48) 으로 양 끝인 47, 48이 가장 높고 중간인 33이 가장 낮을 것을 알 수 있습니다.
즉 우리는 양 끝의 피로도중 큰 값과 중간 값만 구하면 회의 세트에 있던 전체의 피로도에서 단 3번의 피로도만 구하는 것으로 바뀌게 됩니다.
lo_stress = get_stress(lo, hi, lo)
hi_stress = get_stress(lo, hi, hi)
max_stress = max(lo_stress, hi_stress)
mid = (lo + hi) // 2
min_stress = get_stress(lo, hi, mid)
print(max_stress - min_stress)
lo_stress는 가장 앞의 집에서 얻을 수 있는 피로도 이고, hi_stress는 가장 마지막 집에서 얻을 수 있는 피로도 입니다. 이 값이 최대 피로도중 하나입니다. 그리고 가장 낮은 피로도는 중간값인 min_stress를 구해줍니다. 두 값의 차로 회의 세트의 피로도를 구할 수 있습니다. 이렇게 작성하면 총 65점까지 얻을 수 있습니다.
각 집의 피로도 구하기
이제 반복문이 어디에 사용되는지 확인해 보니 각 집의 스트레스를 구할 때 아직 사용되고 있습니다. get_stress 함수를 수정해 보겠습니다.

위 그림과 같이 각 집의 위치를 그래프로 표현해 보았습니다. 각각의 집이 있을 때 파란색 집에서의 피로도를 구해본다고 하겠습니다. 파란색과 각 집의 차이기 때문에 실제 우리가 구하는 피로도의 값은 아래의 노란색과 같습니다.

노란색의 값을 반복문을 통해 매 번 계산해 주었는데 잘 보면 다음과 같은 식으로 나타낼 수 있습니다. 파란색 보다 작은 부분은 처음부터 파란색까지의 사각형에서 처음부터 파란색까지의 합계를 뺀 것과 같습니다. 이를 식으로 나타내 보겠습니다. 시작 값을 i, 마지막 값을 j, 파란색 값을 k라고 하겠습니다.
$$ (k - i) \times x_k - \sum^k_{i=1}x_i $$
파란색보다 큰 부분은 파란색부터 마지막까지의 합계에서 파란색 크기의 사각형을 뺀 것과 같습니다. 식으로 나타내면 다음과 같습니다.
$$ \sum^j_{i=k - 1}x_i - (j - k) \times x_k $$
이것을 식으로 나타내면 다음과 같습니다.
X = [0] + list(mii())
total = []
temp = 0
for x in X:
temp += x
total.append(temp)
def get_stress(i, j, k):
left_stress = (k - i) * X[k] - (total[k] - total[i - 1])
right_stress = (total[j] - total[k - 1]) - (j - k) * X[k]
return left_stress + right_stress
리스트 X의 맨 앞에 0을 추가하였습니다. 누적합을 구할 때 total[i - 1]의 값에서 i가 0일 때 total[-1]이 되기 때문에 마지막 값을 보게 됩니다. 앞에 0을 추가하여 맨 앞을 보는 경우는 0을 만들기 위해 넣은 것입니다.
여기에는 표현되지 않았지만 hi의 값도 수정되어야 합니다.
hi = bisect_right(X, R) - 1
으로 수정 하였습니다. 이전까지는 hi값을 범위로 사용하였기 때문에 -1을 하지 않고 사용했습니다. range의 범위에 마지막값은 들어가지 않기 때문에 -1이 필요 없었습니다. 하지만 여기서는 해당 값을 그대로 사용해야 하기 때문에 -1을 해서 해당 값을 직접 사용할 수 있도록 하였습니다.
다음으로 total 이라는 누적합을 만들어 주었습니다. 반복적인 합을 구할 때에는 누적합이 가장 효과적이기 때문 입니다.
피로도를 절대값을 취하지 않게 하기 위해서 left_stress, right_stress를 각각 구했습니다. 해당 공식은 위에서 구한 공식을 그대로 사용하였습니다. 마지막으로 두 피로도의 합이 해당 집의 피로도가 됩니다.
전체 코드
이렇게 작성한 코드는 100점을 얻을 수 있습니다.
from bisect import bisect_left, bisect_right
import sys
input = sys.stdin.readline
mii = lambda : map(int, input().split())
N, Q = mii()
X = [0] + list(mii())
total = []
temp = 0
for x in X:
temp += x
total.append(temp)
def get_stress(i, j, k):
left_stress = (k - i) * X[k] - (total[k] - total[i - 1])
right_stress = (total[j] - total[k - 1]) - (j - k) * X[k]
return left_stress + right_stress
for _ in range(Q):
L, R = mii()
lo = bisect_left(X, L)
hi = bisect_right(X, R) - 1
if hi <= lo:
print(0)
continue
lo_stress = get_stress(lo, hi, lo)
hi_stress = get_stress(lo, hi, hi)
max_stress = max(lo_stress, hi_stress)
mid = (lo + hi) // 2
min_stress = get_stress(lo, hi, mid)
print(max_stress - min_stress)
문제에서 나온 그대로 구현을 시작으로 5점부터 100점까지 풀이 방법을 알아보았습니다. 시험을 볼 때 처음부터 100점 풀이가 생각난다면 좋겠지만 보통 그렇게 되지는 않습니다. 풀이 방법이 생각나지 않는 어려운 문제를 만난다면 내가 생각한 방향이 맞는지 구현을 해보고, 하나씩 수정해 나가면 100점을 맞지 못해도 부분 점수를 얻을 수 있고, 하나씩 하나씩 수정해 나가면서 100점 풀이로 바꿀 수 있습니다.
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 13306] 트리 (0) | 2025.07.01 |
|---|---|
| [백준 7573] 고기잡이 (2) | 2025.01.27 |
| [백준 10211] Maximum Subarray (0) | 2025.01.19 |
| [백준 1149] RGB 거리 (0) | 2024.12.07 |
| [백준 24552] 올바른 괄호 (4) | 2024.11.27 |


