목차
129회 정보관리기술사 기출 문제로 트리 정렬을 설명하는 문제가 나왔습니다. 알고리즘 문제를 보니 반가운 느낌이 들었습니다.
트리 정렬은 이진 탐색 트리(Binary Search Tree)로 구성한 후 중위 순회 방법으로 순회하면서 오름차순으로 정렬하는 방법 입니다. 이렇게만 들으면 무슨 말인지 잘 이해가 안될 수 있습니다. 하나하나 정리해 보도록 하겠습니다.
트리(Tree) 구조란?
알고리즘에 익숙하다면 트리가 무엇인지 바로 알 수 있지만 알고리즘에 익숙하지 않다면 갑자기 나무가 나와 당황할 수 있습니다.
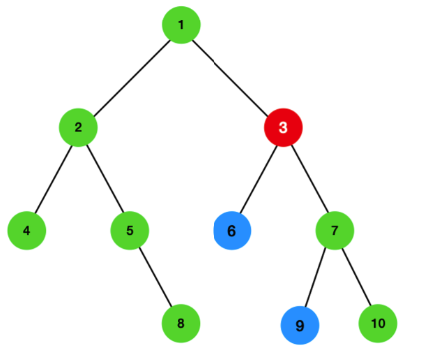
이런 식으로 데이터를 구성하는 방법을 트리 구조라고 합니다. 그림은 최소 공통 조상에 설명했던 그래프를 그냥 가져왔습니다. 색깔이 다른것에 대해 의문을 가질 필요가 없습니다.
숫자가 써 있는 부분이 정점으로 데이터를 저장하는 부분 입니다. 연결된 선이 간선으로 데이터의 연결 구조를 나타냅니다. 트리 구조에는 사이클이 없습니다. 사이클은 어느 정점에서 시작해서 데이터를 타고 가다보면 처음 위치로 돌아오는 경우 입니다. 트리 구조에는 이런 사이클이 존재하지 않습니다. 또 간선은 정점보다 1개 적습니다. 두 개의 정점이 있다면 간선은 한 개 밖에 없습니다. 간선이 2개가 된다면 사이클이 발생하기 때문입니다. 위에서도 10개의 정점이 있어 간선의 개수는 9개가 되는 것입니다.
이진 트리(Binary Tree)란?
이진 트리는 트리의 정점들이 가지는 자식 정점이 최대 두 개 밖에 없는 경우 입니다. 위의 예에서 보인 그래프의 모습이 이진 트리라 할 수 있습니다. 자식 정점이 2개 이상인 것이 있다면 이진 트리라 할 수 없습니다. 반대로 자식이 없거나, 한 개만 있는 경우는 이진 트리라 할 수 있습니다.
이진 탐색 트리(Binary Search Tree) 란?
BST라 불리는 이진 탐색 트리 순서화된 이진 트리 입니다. 정점의 왼쪽 자식은 부모보다 항상 작은 값을 가지고, 오른쪽 자식은 부모보다 항상 큰 값을 가져야 한다는 규칙이 있는 트리 입니다.
트리 탐색 방법
트리를 어떻게 방문하느냐에 따라서 트리 순회 방법의 이름이 다릅니다. 전위 탐색, 중위 탐색, 후위 탐색이라 불리는데 각각 전, 중, 후를 뜻하는 것이 가운데 즉 부모 노드를 언제 방문하느냐에 따라 이름이 달라 집니다. 전위 탐색은 부모 노드를 제일 먼저 방문하고, 중위 탐색은 중간에 부모 노드를 방문하고, 후위 탐색은 가장 마지막에 부모 노드를 방문 하게 됩니다.
전위 탐색(Preorder)
1. 앞의 것 즉 위의 노드를 제일 먼저 방문 합니다.
2. 왼쪽 서브 트리를 Preorder 합니다.
3. 오른쪽 서브 트리를 Preorder 합니다.
위 그래프를 전위 탐색 한다면 1, 2, 4, 5, 8, 3, 6, 7, 9, 10 순서로 방문합니다.
중위 탐색(Inorder)
1. 먼저 왼쪽 서브 트리를 Inorder
2. 가운데 노드 방문
3. 오른쪽 서브 트리 Inorder 합니다.
위 그래프를 중위 탐색 한다면 4, 2, 5, 8, 1, 6, 3, 9, 7, 10 순서로 방문 합니다.
후위탐색(Postorder)
1. 먼저 왼쪽 서브 트리를 Postorder
2. 오른쪽 서브 트리를 Postorder
3. 마지막 중간 노드를 방문 합니다.
위 그래프를 후위 탐색 한다면 4, 8, 5, 2, 6, 9, 10, 7, 3, 1이 됩니다.
시간 복잡도
시간 복잡도는 O(nlogn)입니다.
정리
간단하게 트리정렬에 대해 알아보았습니다. 알고리즘이 특별한 것이 아니기 때문에 따로 알고리즘 문제로 풀어보지는 않겠습니다. 저도 알고리즘 문제를 풀면서 트리 정렬을 이용한 경우는 없었던 것 같습니다.
'IT 지식' 카테고리의 다른 글
| 지지도, 신뢰도, 향상도 (10) | 2023.10.27 |
|---|---|
| ESG 경영 (1) | 2023.10.26 |
| Data Mining 이란? (1) | 2023.10.24 |
| ITSM 이란? (0) | 2023.10.22 |
| SOLID 원칙 (1) | 2023.10.19 |

