목차
문제 출처 : https://www.acmicpc.net/problem/11438
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
앞서 풀어보았던 LCA 문제의 심화 버전 입니다. 입력과 출력의 형식이 똑같지만 주어지는 N과 노드의 쌍 M의 수가 늘어나 있습니다. 따라서 기존의 LCA 문제를 푸는 방식으로는 시간초과가 발생합니다.
LCA의 풀이 방법을 생각해 보겠습니다.
- 두 정점의 깊이를 맞춰 준다.
- 깊이가 같다면 공통 조상이 나올 때까지 하나씩 위로 올라간다.
이 두 가지 방법으로 LCA를 찾아주었습니다. 여기에서는 N과 M이 크기 때문에 깊이를 맞춰주기 위해서 몇 만번의 차이를 하나하나 올라가고, 깊이가 같아지면 공통 조상을 찾기 위해 몇 만번을 하나하나 올라가야 합니다. 결국은 시간초과가 발생할 수 밖에 없습니다. 이렇게 하나하나 올라가는 방식을 빠르게 바꿔줄 수 있는 방법을 생각해야 합니다. 그것이 우리가 잘 알고 있는 이분탐색을 사용하는 것입니다.
지금까지는 부모 정점 하나만을 저장해 놓았지만 이분 탐색에 활용될 수 있도록 2배수의 부모를 저장해 놓는다면 이분탐색에 활용하여 빠르게 부모를 찾을 수 있고, 이분탐색과 같은 형태로 진행되기 때문에 시간도 절약할 수 있습니다.
2배수 부모 저장하기
부모를 이분 탐색할 수 있도록 저장하는 방법에 대해 생각해 보겠습니다.

루트 1부터 시작하여 10번까지 1열로 늘어서 있는 트리가 있습니다. 그림의 자리 차지를 줄이기 위해서 위와 같이 표시 하였습니다. 먼저 기존의 부모 배열을 만들어 보겠습니다. 부모의 초기 세팅으로 생각하면 됩니다.

10번의 부모는 9, 9의 부모는 8.... 2의 부모는 1까지 표현이 되어 있습니다. 1은 루트로 부모가 없기 때문에 빈값으로 해주었습니다. 이제 거리가 2차이 나는 부모를 저장해 보겠습니다. 거리가 2 차이 난다는 것은 결국 부모의 부모입니다. 예를 들어 10번의 부모는 9이기 때문에 9의 부모인 8을 입력 합니다. 이런 식으로 부모의 부모값으로 업데이트를 하면 아래와 같은 모습이 됩니다.

이제 거리가 4 차이가 나는 부모를 저장해 보겠습니다. 거리가 4 차이 난다는 것은 거리가 2 차이나는 부모의 2 차이나는 부모 입니다. 예를 들어 10에서 거리가 2 차이나는 부모는 8 입니다. 이 8의 2차이 나는 부모인 6이 바로 4 차이가 나는 부모 입니다.
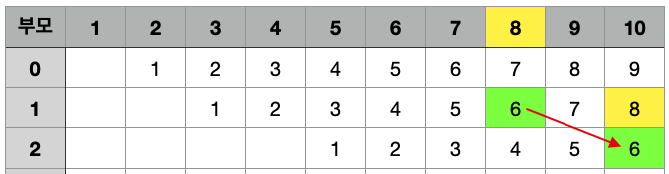
같은 방식으로 8 차이 나는 부모는 4차이 나는 부모의 4 차이 나는 부모가 됩니다. 10의 4 차이 나는 부모인 6의 4 차이나는 부모인 2를 찾아주면 됩니다.

그림으로 알 수 있듯이 쉽게 2배수 차이나는 부모를 쉽게 찾을 수 있습니다. DP와 같은 형태로 부모 리스트의 점화식을 다음과 같이 만들 수 있습니다.
prt = parent[j][i - 1]
parent[j][i] = parent[prt][i - 1]여기서 j는 정점을 뜻하고 i는 몇 배수 부모인지를 나타냅니다. 예를 들어 10번의 2^3인 부모를 찾기 위해서는 2^2 배수 부모부터 먼저 찾아야 합니다. parent[10][2]는 6으로 prt는 6이 됩니다. 다음으로 6의 2^2 배수 부모는 parent[6][2]로 2가 됩니다. 즉 parent[10][3]은 2가 되는 것입니다.
문제 풀어보기
그럼 앞에서 배운 내용을 생각하면서 문제를 풀어보도록 하겠습니다.
입력 받기
import sys
sys.setrecursionlimit(10 ** 5)
input = sys.stdin.readline
mii = lambda : map(int, input().split())
N = int(input())
tree = [[] for _ in range(N + 1)]
for _ in range(N - 1):
u, v = mii()
tree[u].append(v)
tree[v].append(u)두 번째 줄은 트리의 깊이가 깊어졌기 때문에 그냥 문제를 풀면 재귀 요류가 발생합니다. 그래서 미리 재귀의 한계를 늘려 주었습니다. 그리고 입력되는 양이 많기 때문에 readline을 사용하도록 하였습니다. 입력은 정점의 개수 N과 트리의 정보를 입력 받았습니다. 여기까지는 별 다른 점이 없습니다.
부모 정점과 정점의 깊이 구하기
depth = [-1] * (N + 1)
def dfs(nd, lv):
depth[nd] = lv
for nxt in tree[nd]:
if depth[nxt] == -1:
parent[nxt][0] = nd
dfs(nxt, lv + 1)
def set_parents():
dfs(1, 0)
set_parents()set_parents 함수를 실행하면 dfs가 돌면서 부모 정점과 정점의 깊이를 알 수 있습니다. 여기는 앞서 풀었던 문제와 별 차이가 없습니다. 이 로직이 이해 되지 않는다면 LCA 문제를 풀어보고 오시길 바랍니다. LCA에서는 parent[nxt]로 저장한 것을 여기서는 2차원 배열로 만들기 위해서 parent[nxt][0]에 저장하였습니다.
이제 DP를 응용한 방법으로 부모의 부모들을 저장해 놓는 로직을 추가해 보겠습니다.
트리 깊이 구하기
트리의 깊이를 구하는 방법은 2배수씩 트리의 크기를 늘려가면서 어느 정점까지 포함되는지 확인하는 방식으로 하였습니다. 이진 트리가 아닌데 2배수씩 늘리는 이유는 최대한 트리의 크기를 크게 해놔야 나중에 범위를 벗어나지 않기 때문 입니다.
size = 0
tot_depth = 1
while True:
if N < size:
break
size += 1 << tot_depth
tot_depth += 1트리의 사이즈를 구하는 방법은 세그먼트 트리나 K진 트리 문제에서 설명하였기 때문에 넘어가겠습니다. 2의 배수를 대충 외우고 있다면 트리의 깊이를 20정도만 해도 충분합니다. 2의 20승은 약 100만보다 조금 더 큰 정도이기 때문에 100만 이하라면 트리의 깊이를 20으로 하면 됩니다.
부모의 부모 저장하기
parent = [[0] * tot_depth for _ in range(N + 1)]
def set_parents():
dfs(1, 0)
for i in range(1, tot_depth):
for j in range(1, N + 1):
prt = parent[j][i - 1]
parent[j][i] = parent[prt][i - 1]다음으로 부모의 부모를 저장하는 로직 입니다. 이 로직은 위에서 설명하였습니다. DP로 부모의 부모를 저장하면 자연스럽게 2배수씩 늘어나 이분탐색이 쉽게 가능합니다.
쿼리 수행하기
M = int(input())
for _ in range(M):
a, b = mii()
print(lca(a, b))총 M개의 쿼리를 수행합니다. 입력받은 a, b를 lca 함수를 통해 거리를 구해 줍니다.
lca 함수
def lca(a, b):
if depth[b] < depth[a]:
a, b = b, a
for i in range(tot_depth - 1, -1, -1):
if (1 << i) <= depth[b] - depth[a]:
b = parent[b][i]
if a == b:
return a
for i in range(tot_depth - 1, -1, -1):
if parent[a][i] != parent[b][i]:
a = parent[a][i]
b = parent[b][i]
return parent[a][0]lca 함수는 기존 LCA와 비슷합니다. 먼저 깊이를 맞춰주기 위해서 a와 b의 깊이를 비교해서 설정한 것과 틀리다면 바꿔줍니다. 저는 a가 더 짧다고 가정하였습니다. 즉 b 정점을 a의 정점 깊으로 먼저 맞춰주어야 합니다.
깊이를 맞추는 방식도 1씩 올라가는 것이 아니라 2배수씩 올라갑니다. 1 << i를 사용하여 이분 탐색식으로 올라가기 때문에 빠르게 두 정점의 깊이를 맞출 수 있습니다.
다음으로 같은 최소 공통 조상이 나올 때까지 같이 올라갑니다. 여기서도 parent에 2배수씩 저장되어 있기 때문에 이분 탐색과 같이 빠르게 최소 공통 조상을 찾을 수 있습니다.
전체 코드
전체 코드를 확인해 보겠습니다.
import sys
sys.setrecursionlimit(10 ** 5)
input = sys.stdin.readline
mii = lambda : map(int, input().split())
N = int(input())
tree = [[] for _ in range(N + 1)]
for _ in range(N - 1):
u, v = mii()
tree[u].append(v)
tree[v].append(u)
size = 0
tot_depth = 1
while True:
if N < size:
break
size += 1 << tot_depth
tot_depth += 1
depth = [-1] * (N + 1)
parent = [[0] * tot_depth for _ in range(N + 1)]
def dfs(nd, lv):
depth[nd] = lv
for nxt in tree[nd]:
if depth[nxt] == -1:
parent[nxt][0] = nd
dfs(nxt, lv + 1)
def set_parents():
dfs(1, 0)
for i in range(1, tot_depth):
for j in range(1, N + 1):
prt = parent[j][i - 1]
parent[j][i] = parent[prt][i - 1]
set_parents()
def lca(a, b):
if depth[b] < depth[a]:
a, b = b, a
for i in range(tot_depth - 1, -1, -1):
if (1 << i) <= depth[b] - depth[a]:
b = parent[b][i]
if a == b:
return a
for i in range(tot_depth - 1, -1, -1):
if parent[a][i] != parent[b][i]:
a = parent[a][i]
b = parent[b][i]
return parent[a][0]
M = int(input())
for _ in range(M):
a, b = mii()
print(lca(a, b))
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 1504] 특정한 최단 경로 (0) | 2023.12.09 |
|---|---|
| [백준 10808] 알파벳 개수 (0) | 2023.11.23 |
| [백준 24955] 숫자 이어 붙이기 (0) | 2023.11.10 |
| [백준 11812] K진 트리 (1) | 2023.11.06 |
| [백준 4195] 친구 네트워크 (0) | 2023.10.13 |


