목차
문제 출처 : https://www.acmicpc.net/problem/1504
1504번: 특정한 최단 경로
첫째 줄에 정점의 개수 N과 간선의 개수 E가 주어진다. (2 ≤ N ≤ 800, 0 ≤ E ≤ 200,000) 둘째 줄부터 E개의 줄에 걸쳐서 세 개의 정수 a, b, c가 주어지는데, a번 정점에서 b번 정점까지 양방향 길이 존
www.acmicpc.net
문제 설명
최단 경로를 구하는 다익스트라 알고리즘 문제 입니다. 다익스트라 알고리즘에 대해서 잘 모른다면 아래 링크를 통해 확인해 보시기 바랍니다.
01. 다익스트라 알고리즘
# 다익스트라 알고리즘 다익스트라 알고리즘(Dijkstra Algorithm)은 그래프에서 최단 경로를 구하는 알고리 즘입니다. BFS알고리즘을 배울 때 이미 BFS 알고리즘이 …
wikidocs.net
최단 경로를 구하는데 그냥 구하는 것이 아니라 특정한 경로를 지나는 최단 경로를 구하는 것입니다. 문제의 예로 확인해 보겠습니다.
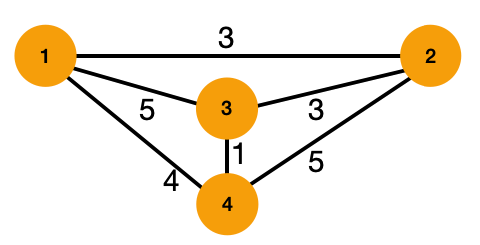
다음과 같은 경로가 있고 여기서 시작인 1부터 마지막 정점인 4까지의 거리를 구하는 것입니다. 그냥 구하는 것이 아니라 특정한 경로를 지나야 합니다. 예에서는 2에서 3번의 경로를 무조건 지나야 합니다. 원래 1부터 4까지의 최단 거리는 4이지만 이 문제에서는 2에서 3을 지나야 하기 때문에 1 - 2 - 3 - 4 순으로 지나면 7이 최단 경로가 됩니다.
이해하기
최단 경로를 구하는 다익스트라 알고리즘을 사용하여 특정 경로를 지나게 하는 방법은 없습니다. 이렇게 복잡한 문제를 만나면 문제를 작게 나누는 것이 해답이 될 수 있습니다. 여기서도 1부터 N까지 경로중에서 V1 - V2 경로를 포함하는 최단 경로라고 생각하면 어렵습니다. 문제를 작게 쪼개서 1부터 V1, V1부터 V2, V2에서 N까지의 최단 경로의 합계라고 생각하면 문제가 쉬워집니다. 그럼 기존에 사용하던 최단 경로 알고리즘을 그대로 사용하면서 특정 경로를 포함하는 최단 경로를 구할 수 있게 됩니다.

한가지 추가하자면 1 - V1 - V2 - N 순의 최단 경로라고 말했지만 이것이 최단 경로가 아닐 수 있습니다. 바로 1 - V2 - V1 - N 순서로 방문하는 것이 더 짧은 최단 경로가 될 수도 있습니다. 따라서 이 두가지 경우를 모두 확인해주어야 합니다.
문제 풀이
그럼 코드를 직접 작성해 보겠습니다.
입력 받기
mii = lambda : map(int, input().split())
N, E = mii()
arr = [[] for _ in range(N + 1)]
for _ in range(E):
a, b, c = mii()
arr[a].append((b, c))
arr[b].append((a, c))
v1, v2 = mii()첫째줄에 정점의 개수 N과 간선의 개수 E를 입력 받습니다. 다음으로 그래프의 정보를 입력 받습니다. 두 정점 a, b와 그 사이의 거리 c를 입력 받아 그래프를 구성해 주었습니다. 마지막으로 특정 경로인 v1, v2를 입력 받습니다.
다익스트라 함수 만들기
최단 경로를 구하는 다익스트라 함수를 만들어 보겠습니다.
from heapq import heappop, heappush
INF = float("INF")
def dijkstra(s):
dist = [INF] * (N + 1)
q = [(0, s)]
dist[s] = 0
while q:
curr_dist, node = heappop(q)
if dist[node] < curr_dist:
continue
for nxt_node, nxt_dist in arr[node]:
distance = curr_dist + nxt_dist
if distance < dist[nxt_node]:
dist[nxt_node] = distance
heappush(q, (distance, nxt_node))
return dist우선 순위 큐를 사용할 예정이기 때문에 heapq를 import하였습니다. 다익스트라 함수에 대해서는 위 링크에서 설명하였기 때문에 따로 설명하지 않겠습니다. 최종적으로 시작 정점 s에서의 최단 경로를 저장한 리스트를 리턴합니다.
문제 풀이
start_1 = dijkstra(1)
start_v1 = dijkstra(v1)
start_v2 = dijkstra(v2)
dist1 = start_1[v1] + start_v1[v2] + start_v2[N]
dist2 = start_1[v2] + start_v2[v1] + start_v1[N]
ans = min(dist1, dist2)
if ans == INF:
print(-1)
else:
print(ans)
다익스트라 알고리즘을 사용하여 최단 경로를 구해주었습니다. 위에서 말했듯이 경로를 쪼개어 시작위치가 다른 각각의 다익스트라 최단 경로를 구했습니다. start_1은 1번 정점에서 시작하는 최단 경로 입니다. start_v1은 v1 정점에서 시작하는 최단 경로이고, start_v2는 v2 정점에서 시작하는 최단 경로 입니다.
이제 거리를 구해야 하는데 1 - V1 - V2 - N 만 확인하는 것이 아니라 1 - V2 - V1 - N 역시 확인해야 한다고 했습니다. 그래서 dist1에는 1 - V1 - V2 - N 순으로 방문한 최단 경로를 구해주었고, dtst2는 1 - V2 - V1 - N 으로 최단 경로를 구했습니다. 최종적으로 ans에 최단 경로 정보가 저장됩니다.
문제의 마지막에는 최단 경로가 없는 경우 -1을 출력하라고 하였습니다. 만약 경로가 없다면 ans 값은 무한대 값인 INF 가 될 것입니다. 따라서 ans 값이 INF라면 -1을 출력하고 아닐 경우 정상적인 ans 값을 출력하는 것입니다.
전체 코드
전체 코드를 확인해 보겠습니다.
from heapq import heappop, heappush
INF = float("INF")
mii = lambda : map(int, input().split())
N, E = mii()
arr = [[] for _ in range(N + 1)]
for _ in range(E):
a, b, c = mii()
arr[a].append((b, c))
arr[b].append((a, c))
v1, v2 = mii()
def dijkstra(s):
dist = [INF] * (N + 1)
q = [(0, s)]
dist[s] = 0
while q:
curr_dist, node = heappop(q)
if dist[node] < curr_dist:
continue
for nxt_node, nxt_dist in arr[node]:
distance = curr_dist + nxt_dist
if distance < dist[nxt_node]:
dist[nxt_node] = distance
heappush(q, (distance, nxt_node))
return dist
start_1 = dijkstra(1)
start_v1 = dijkstra(v1)
start_v2 = dijkstra(v2)
dist1 = start_1[v1] + start_v1[v2] + start_v2[N]
dist2 = start_1[v2] + start_v2[v1] + start_v1[N]
ans = min(dist1, dist2)
if ans == INF:
print(-1)
else:
print(ans)'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 1219] 오민식의 고민 (1) | 2024.01.01 |
|---|---|
| [백준 1865] 웜홀 - 플로이드 워셜 풀이 (1) | 2023.12.17 |
| [백준 10808] 알파벳 개수 (0) | 2023.11.23 |
| [백준 11438] LCA 2 (1) | 2023.11.15 |
| [백준 24955] 숫자 이어 붙이기 (0) | 2023.11.10 |


