목차
2022년도 정보올림피아드 2차 데회에서 초등부, 중등부, 고등부 모두 나왔던 문제입니다. 그럼 같이 풀어보도록 하겠습니다.
문제의 예제를 살펴 보겠습니다. 아래와 같이 연결 되어 있는데 S = {1, 2, 3, 4, 5, 6} 입니다. 7만 연결이 안되어 있는 상태 입니다. 이것을 아래와 같이 표현할 수 있습니다.
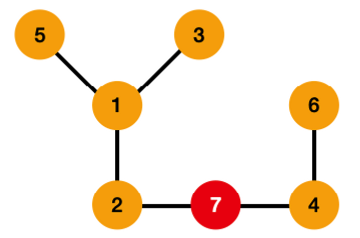
연결되어 있는 노드들을 확인해보면 다음과 같습니다.
(1 - 2), (1 - 3), (1 -5), (2 - 3), (2 - 5), (3 - 5), (4 - 6)
이렇게 7개가 연결 되어있고, 연결강도가 7임을 확인할 수 있습니다. 즉 각 노드들이 연결 되어 있는 노드들의 갯수를 확인하는 것이 이 문제 입니다.
모두 구해보기
가장 쉽게 생각하면 S에 포함된 노드들이 각각 연결되어 있는지 확인하여 연결 되어 있으면 1씩 추가하면 됩니다. 그럼 간단한 방법으로 문제를 풀어 보도록 하겠습니다.
입력 받기
모두 구하기 위해서 입력을 받아보도록 하겠습니다.
N = int(input())
arr = [[] for _ in range(N+1)]
for _ in range(N-1):
u, v = map(int, input().split())
arr[u].append(v)
arr[v].append(u)
N의 입력을 받고 인접 리스트 형태로 arr이라는 트리를 구성 하였습니다.
쿼리 입력 받기
Q = int(input())
for _ in range(Q):
K, *S = list(map(int, input().split()))
not_in_S = [True] * (N + 1)
for s in S:
not_in_S[s] = False
ans = 0
for i in range(K - 1):
for j in range(i+1, K):
visited = not_in_S[:]
ans += dfs(S[i], S[j])
print(ans)
쿼리의 갯수 Q를 입력 받습니다. 반복문을 통해 각각의 쿼리 입력 받기를 Q번 반복합니다. 이 때 입력된 쿼리의 형태가 먼저 쿼리의 갯수 K, 그 다음에 실제 쿼리가 입력되기 때문에 K와 *S로 입력을 받습니다.
다음으로 S 안에 포함된 항목들만 방문하도록 해야 하기 때문에 포함되지 않은 나머지 항목들을 전부 not_in_S 에서 True로 처리 합니다. 이제 S에 있는 항목들만 not_in_S에서 False 이기 때문에 해당 항목들로 dfs 탐색을 할 수 있습니다.
dfs는 S안에 있는 요소들을 2개씩 짝을지어 연결이 되어 있는지 확인하는 코드를 작성합니다. 이 때 not_in_S 리스트를 활용하여 visited 리스트로 사용합니다. 두 요소를 비교할 때 visited 리스트가 초기화 되어야 하기 때문에 매 번 not_in_S 리스트를 복사합니다. 그냥 visited = not_in_S로 하게되면 복사가 아닙니다. not_in_S 뒤에 [:]를 붙여주어야 얕은 복사가 되고 visited 리스트를 수정해도 not_in_S 리스트에 영향을 받지 않게 됩니다.
dfs 함수는 최종적으로 두 정점이 연결되어 있으면 1을, 아니면 0을 리턴합니다. 연결되어 있는 최종 정보 ans가 답이 되게 됩니다. 그럼 dfs 함수를 만들어 보도록 하겠습니다.
dfs 함수 만들기
def dfs(s, e):
visited[s] = True
cnt = 0
for a in arr[s]:
if a == e:
return 1
if visited[a] == False:
cnt += dfs(a, e)
return cnt
먼저 자신이 해당 노드에 방문했다고 visited 리스트에 True 처리를 해줍니다. 다음으로 s와 e가 같을 경우 두 노드가 연결되어 있다는 것이기 때문에 1을 리턴합니다. 아직 e에 도달하지 못하였다면 visited 리스트를 확인하여 방문을 계속하면서 두 노드가 만날 때까지 탐색을 이어나갑니다. 최종적으로 e노드에 도달하지 못하면 0이 리턴될 것입니다.
수학적인 방법 추가하기
위와 같이 문제를 해결하면 10점을 받을 수 있습니다. N과 Q가 50개 이하일 때에만 동작하는 것입니다. 방문을 하는데 너무 시간이 많이 걸리기 때문입니다. 매 번 두 노드가 연결되어 있는지 확인하는 코드는 시간이 오래 걸릴 수 밖에 없습니다. 그렇기에 dfs로 방문 가능한 노드를 구한 다음에 해당 노드로 연결 가능한 갯수를 찾는 것이 더 빠릅니다.
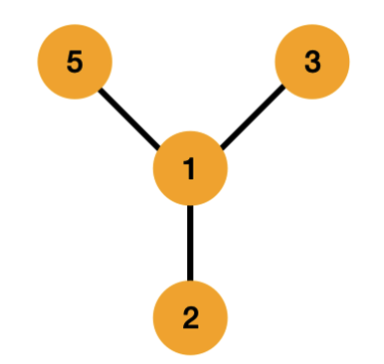
앞에서는 각 노드들이 연결되어 있는지 아닌지 모두 직접 확인하였습니다. 이번에는 노드들의 갯수를 구해서 노드의 갯수 2개가 가능한 경우의 수를 수학적으로 구해줍니다. 4개가 연결 되어 있기 때문에 $_nC_r$ 로 갯수를 구할 수 있습니다. 공식은 n * (n-1) / 2를 사용하면 됩니다. $_4C_2$를 계산하면 4 * 3 / 2 로 6개를 구할 수 있습니다.
수학적 로직 추가하기
Q = int(input())
for _ in range(Q):
K, *S = list(map(int, input().split()))
visited = [True] * (N + 1)
for s in S:
visited[s] = False
result = 0
for s in S:
if visited[s] == False:
ans = dfs(s)
result += ans * (ans - 1) // 2
print(result)
아까와는 비슷하지만 반복문이 줄었습니다. 두 노드가 연결되어 있는지 확인하는 것이 아니라 dfs를 통해 노드의 갯수를 구해줍니다. 그리고 거기서 나온 갯수를 수학적으로 계산하여 result를 구합니다. 그럼 노드의 갯수를 구하는 dfs 함수를 구현해 보겠습니다.
dfs 함수 구현
def dfs(s):
visited[s] = True
cnt = 1
for a in arr[s]:
if visited[a] == False:
cnt += dfs(a)
return cnt
노드들을 방문할 때마다 cnt를 하나씩 늘려나가는 로직으로 변경 하였습니다. 좀 전과 다른 점은 시작과 끝을 통해 노드가 연결되어 있는 것이 아니라 노드를 만날 때마다 cnt를 늘려줍니다.
이렇게 만들어도 만점은 아닌 21점밖에 얻을 수 없습니다. N과 Q가 2,500개는 처리가 가능하지만 250,000개 처리는 아직 되지 않습니다. dfs로 노드들의 연결 정보를 매번 구하는 방법이 아닌 다른 방법이 필요합니다. 트리나 그래프에서 노드들의 연결 정보를 확인하기 좋은 방법중 하나가 바로 유니온 파인드 입니다. 우리는 이 로직을 유니온 파인드로 변경하여 생각할 필요가 있습니다.
Union Find 사용하기
유니온 파인드는 여러 노드중 두 노드가 연결 되어 있는지, 아닌지만을 알고 싶을 때 사용 합니다. 이 문제에서는 노드간의 연결이 어떻게 되어 있는지는 상관 없습니다. 아래와 같이 2번과 5번의 부모를 확인하여 부모가 같으면 연결되어 있다고 생각하는 것이 유니온 파인드의 핵심입니다.
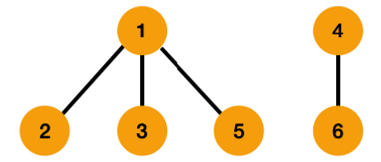
그럼 이렇게 노드들을 나누는 기준이 무엇이 될 수 있을지 생각해 보겠습니다. 먼저 그래프를 트리 형태로 만들어 줍니다.

다음으로 자신과 트리부모 둘 다 S에 포함 되어 있는지 확인합니다. 포함 되어 있으면 Union 해주고, 포함되어 있지 않으면 넘어 갑니다.

처음에는 자기 자신이 부모입니다. 2와 2의 트리부모인 1은 같은 S안에 포함 되어 있기 때문에 Union 합니다. 이렇게 3, 5도 S안에 속하기 때문에 모두 Union 합니다.

4의 트리부모는 7 입니다. 7은 S에 포함되어 있지 않기 때문에 Union 하지 않습니다.
6의 트리부모는 4 입니다. 4는 S에 포함되어 있기 때문에 Union 합니다. 그리고 7은 S에 없기 때문에 사용하지 않습니다.

유니온 파인드를 통해 위와 같은 관계를 구할 수 있습니다. 1의 자식 노드들은 총 4개, 4의 자식 노드들은 2개입니다. 4 * (4-1) / 2를 통해 6을 구할 수 있고, 2 * (2-1) / 2를 통해 1을 구할 수 있습니다. 노드들을 통해 구한 값의 합인 7이 정답이 됩니다.
import sys
input = sys.stdin.readline
N = int(input())
tree = [0] * (N+1)
def dfs(s):
visited[s] = True
q = [s]
while q:
node = q.pop()
for next in arr[node]:
if visited[next]:
continue
tree[next] = node
visited[next] = True
q.append(next)
def find(n):
if parent[n] != n:
parent[n] = find(parent[n])
return parent[n]
def union(a, b):
pa = find(a)
pb = find(b)
if pa == pb:
return
cnt[pa] += cnt[pb]
parent[pb] = pa
arr = [[] for _ in range(N+1)]
for _ in range(N-1):
u, v = map(int, input().split())
arr[u].append(v)
arr[v].append(u)
visited = [False] * (N+1)
dfs(1)
Q = int(input())
inS = [False] * (N+1)
cnt = [1] * (N+1)
parent = list(range(N+1))
for _ in range(Q):
K, *S = list(map(int, input().split()))
for s in S:
inS[s] = True
for s in S:
if inS[tree[s]]:
union(s, tree[s])
result = 0
for s in S:
if find(s) == s:
result += cnt[s] * (cnt[s] - 1) // 2
inS[s] = False
parent[s] = s
cnt[s] = 1
print(result)
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 28219] 2023 정올 1차 주유소 (1) | 2023.08.23 |
|---|---|
| [백준 1655] 가운데를 말해요 (0) | 2023.08.22 |
| [백준 28326] 2023 정올 고기파티 (0) | 2023.08.21 |
| [백준 22344] 2021 정올 그래프 균형 맞추기 (0) | 2023.08.16 |
| [백준 21762] 2021 정올 공통 부분 수열 확장 (0) | 2023.08.15 |



