목차
문제 출처 : https://www.acmicpc.net/problem/28326
28326번: 고기 파티
오늘은 고기 파티가 열리는 날이다. 파티에 걸맞도록, 기다란 그릴 위에 잘 구워진 고기가 총 $N$개 놓여 있다. 그릴을 $10^9$ 의 길이를 가진 선분이라고 하고, 그릴의 왼쪽 끝을 좌표 $0$, 오른쪽
www.acmicpc.net
이 문제는 2023년도 정보 올림피아드 2차 초등부 4번, 중등부 3번 문제 입니다.
문제의 이해
먼저 문제를 이해하도록 해보겠습니다. 첫 번째 예제를 함께 보면서 무엇을 해야하는지 알아보겠습니다.

이와같이 그릴에 고기가 쌓여 있습니다. 여기서 왼쪽 오른쪽에 꼬치를 꽂고 가져갑니다. 가져간 고기들의 맛의 합을 구하는 문제 입니다. 이 때 꼬치 양쪽 모두에 꽂힌 고기만 가져갈 수 있고, 하나만 꽂힌 고기는 떨어뜨리게 됩니다. 여러번 이 작업을 시행 하였을 때 각각의 고기 맛의 합계를 구하면 됩니다.
먼저 3, 6에 꼬치를 꽂습니다. 문제는 꼬치의 위치가 정확히 3이 아니라 왼쪽 꼬치는 3 + 0.1, 오른쪽 꼬치는 6 + 0.9 입니다. 즉 꼬치를 가져오는 범위가 왼쪽은 3을 초과하고 오른쪽은 7미만인 고기 입니다.
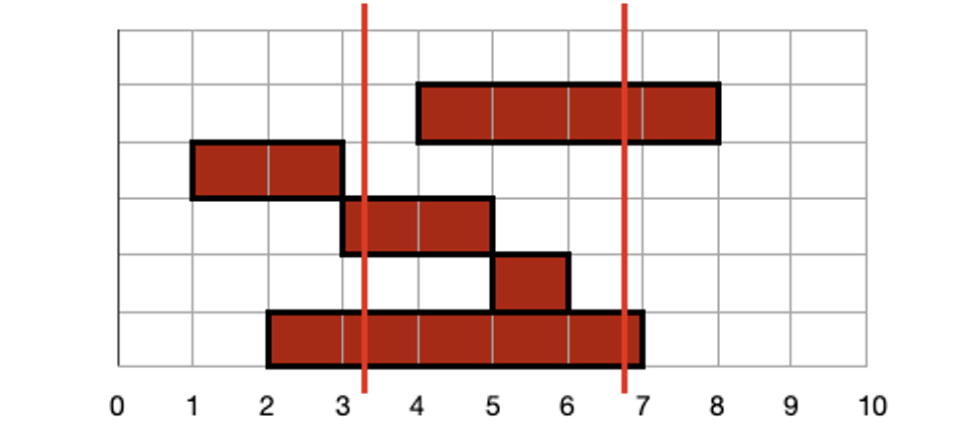
꼬치가 둘 다 꽂혀있는 첫 번째 고기는 가져갈 수 있습니다. 그래서 첫 번째 꼬치로 얻는 고기 맛은 3이 됩니다. 하지만 3, 4, 5에 위치한 고기들은 하나의 꼬치만 꽂혀있기 때문에 바닥에 떨어지고 사라집니다.

다음 2와 4의 꼬치에는 하나의 고기만 꽂혀 바닥에 떨어지기 때문에 0이 됩니다. 마지막으로 5 5의 꼬치는 5.1, 5.9의 위치에 꼬치를 꽂아 마지막 고기를 가져갈 수 있고, 고기맛은 9가 됩니다.

무작정 해보기
문제를 이해했으니 브루트포스로 무작정 실행하는 방법부터 시도해 보겠습니다. 100점을 맞지 못하더라도 부분 점수를 받을 수 있다면 단 5점이라도 받는 것이 중요합니다. 실제 대회에서 같은 점수임에도 실행 속도에 따라 순위가 갈리고, 상의 이름이 바뀌는 경우를 많이 보았기 때문 입니다.
입력 받기
import sys
input = sys.stdin.readline
mii = lambda : map(int, input().split())
N, M = mii()
arr = []
for _ in range(N):
s, e, t = mii()
arr.append([s, e, t])
for _ in range(M):
x, y = mii()
print(solve(x, y))
입력 받는 숫자가 많기 때문에 readline을 사용하여 속도를 높여주었습니다. 다음으로 map(int, input().split())을 여러번 사용하는 것이 귀찮아서 lambda를 이용하여 mii라는 함수로 만들어 주었습니다.
다음으로 고기의 수 N과 사람의 수 M을 입력 받습니다. 다음으로 고기의 크기 시작 start의 약자로 s, 끝 end의 약자 e, 맛 taste의 약자 t로 입력 받습니다. 입력 받은 내용은 arr이라는 리스트에 저장해 놓습니다.
다음으로 사람의 수 M횟수 만큼 반복하여 꼬치의 시작과 끝인 x, y를 입력 받습니다. 꼬치의 시작값과 끝값을 이용한 함수 solve를 사용하여 문제를 해결할 것입니다.
solve 함수 작성
다음으로 solve(x, y)함수를 작성해 보겠습니다.
def solve(x, y):
taste = 0
for i in range(N):
s, e, t = arr[i]
check = 0
if s <= x < e:
check = 1
if s <= y < e:
check += 1
if check:
arr[i][0] = -1
arr[i][1] = -1
if check == 2:
taste += t
return taste
모든 고기들을 탐색 하면서 꼬치에 꽂히는 고기를 찾습니다. x 꼬치는 시작 s가 x보다 작은 모든 꼬치에 꽂힙니다. 이 때 x가 3이라면 3이 포함된 꼬치도 꽂히기 때문에 s ≤ x 가 됩니다. 다음으로 끝 위치는 3이 포함되지 않기 때문에 x < e가 됩니다. y값 역시 똑같은 방법으로 꼬치에 꽂힌 항목을 찾습니다.
check값이 1보다 크면 고기가 꼬치에 꽂힌것이기 때문에 바닥에 떨어지거나, 사람들이 먹은 것입니다. 따라서 더 이상 탐색이 되지 않도록 시작과 끝 값을 -1로 변경 합니다. check 값이 2인 경우는 양쪽 꼬치 모두 꽂힌 것이기 때문에 사람들이 먹을 수 있습니다. 따라서 그 고기의 맛을 taste값에 더해줍니다.
모든 탐색이 끝나고 taste값을 리턴해주면 됩니다. 이렇게 제출하면 5점을 얻을 수 있습니다. 매번 모든 고기들을 체크하기 때문에 속도가 느릴 수밖에 없습니다. 따라서 좀 더 빠른 방법을 고민해야 합니다.
고기 정렬해보기
조금 더 빠른 방법을 사용하기 위해 고기들을 정렬하여 위치를 찾는다면 좀 더 빠를 것 같아 보입니다. 먼저 시작 위치를 기준으로 모든 고기를 정렬 합니다.

이제 왼쪽 꼬치는 해결 되었습니다. 첫 번째 꼬치인 (3, 6)을 기준으로 생각해보면, 고기의 시작이 3이하인 항목들 중에서 오른쪽 꼬치인 6보다 큰 항목을 조회하면 양쪽 꼬치에 모두 꽂힌 고기들을 찾을 수 있습니다.

시작이 3보다 작은 고기는 총 3개가 있고, 첫 번째 고기는 6보다 작기 때문에 선택되지 않습니다. 두 번째 고기는 끝 위치가 6보다 크기 때문에 선택 됩니다. 세 번째 고기도 6보다 작기 때문에 선택되지 않습니다.
추가적으로 네 번째 고기는 시작 범위에서 벗어나기 때문에 6보다 크기는 하지만 조회 범위에 없어 선택되지 않습니다.
문제는 시작 위치는 정렬 되었지만 끝 위치는 정렬되지 않았기 때문에 찾는데 시간이 오래 걸릴 수 밖에 없습니다. 끝 부분을 빨리 찾기 위해 세그먼트 트리를 사용해야 합니다. 정렬된 범위로 시작이 3보다 작은 고기들 중에서 6보다 큰 고기들만 선택하면 됩니다. 고기맛은 3이기 때문에 3을 출력 합니다.
꼬치에 꽂힌 고기는 세그먼트 트리의 업데이트를 통해 길이를 -1로 변경 합니다.

똑같은 방식으로 고기의 시작이 3이하이면서 4이하인 고기들을 삭제합니다. 이 고기들은 왼쪽 꼬치에 찔려 바닥에 떨어진 고기 입니다.

다음으로 오른쪽 꼬치인 6 이하의 항목들중 7보다 작은 고기들을 제외시켜 줍니다. 이 고기들은 오른쪽 꼬치에만 꽂혀 바닥에 떨어진 고기 입니다.
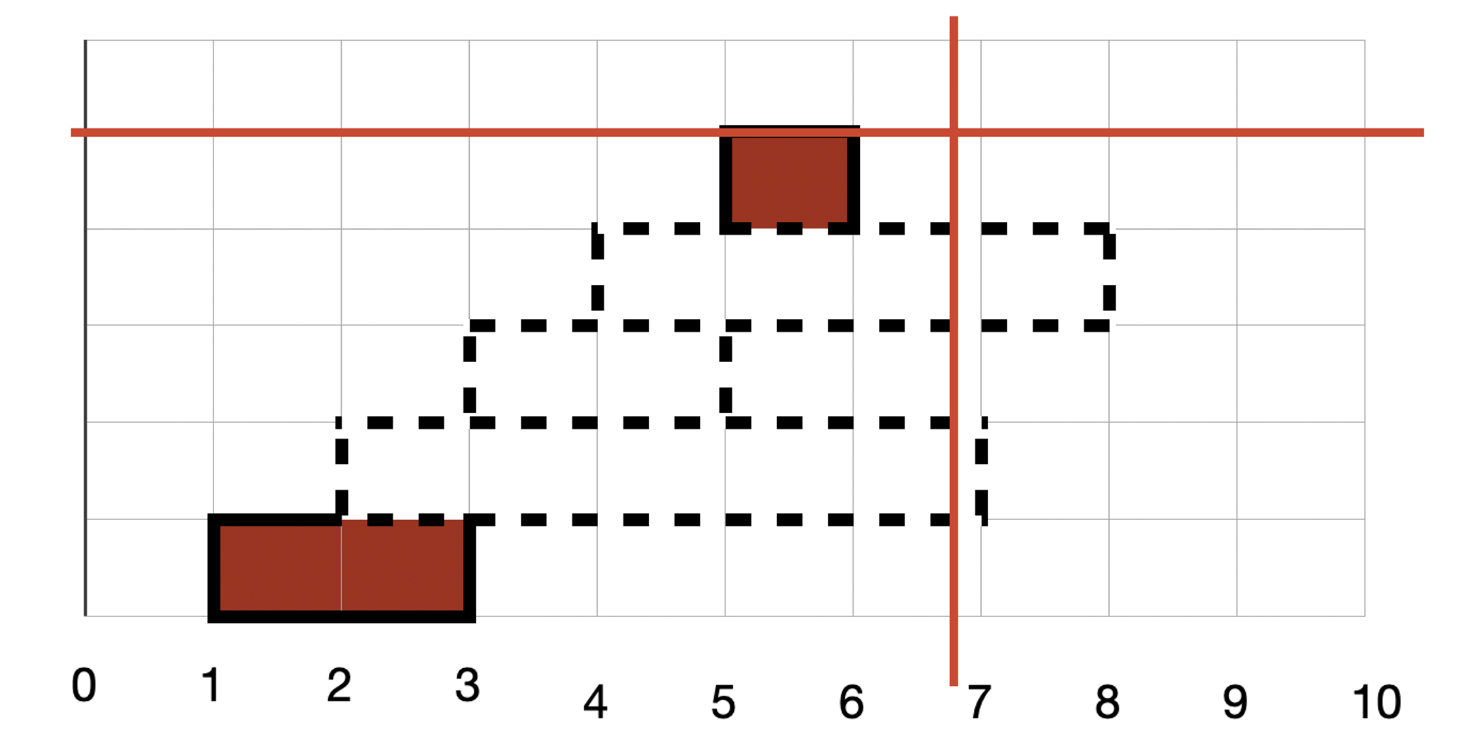
다음으로 (2, 4) 꼬치를 꽂습니다. 시작이 2보다 작은 항목들 중 길이가 4보다 큰 고기를 찾습니다.

고기가 없기 때문에 고기 맛의 합계는 0을 출력 합니다. 꼬치에 꽂히지 않았기 때문에 업데이트 되는 항목은 없습니다.
다음으로 왼쪽 꼬치에 꽂힌 고기들을 제외 합니다. 2보다 작은 항목들 중에서 3보다 큰 고기들을 삭제하면 됩니다.

오른쪽 꼬치인 4의 항목을 삭제하기 위해 4보다 작은 항목들 중에서 5 이상인 항목을 삭제합니다. 여기에는 삭제되는 항목이 없습니다.

마지막 (5, 5) 꼬치를 꽂습니다. 5 이하의 항목들 중에서 6 이하의 항목을 고르면 됩니다. 하나 남은 고기의 맛인 9를 출력 합니다.

이 과정들을 정리하면 이렇습니다.
- 고기의 시작 값 s로 정렬을 한다.
- 고기의 끝 값 e로 세그먼트 트리를 만든다.
- 꼬치의 시작값 s를 이분 탐색으로 세그먼트 트리를 탐색할 끝 값인 last_s를 찾습니다.
- 0부터 last_s 사이에서 e보다 큰 항목을 모두 고릅니다.
- 4번에서 고른 모든 항목의 고기 맛을 더하여 출력합니다.
- 4번 항목들의 끝값을 -1로 변경합니다.
- last_s 이하의 항목들 중 s + 1보다 큰 모든 고기는 왼쪽 꼬치로 떨어뜨린 고기이므로 삭제합니다.
- 꼬치의 끝 값 e를 이분 탐색으로 e의 범위 값 last_e를 찾습니다.
- last_e보다 작은 항목들 중 e + 1보다 큰 고기는 오른쪽 꼬치로 떨어뜨린 고기이므로 삭제합니다.
- 다음 꼬치값이 들어오면 3번부터 다시 실행 합니다.
그럼 코드로 작성해 보겠습니다.
입력 받기
import sys
input = sys.stdin.readline
mii = lambda : map(int, input().split())
N, M = mii()
arr = []
sidx = []
for _ in range(N):
s, e, t = mii()
arr.append((s, e, t))
sidx.append(s)
arr.sort()
sidx.sort()
입력량이 많기 때문에 readline으로 속도를 높여주었습니다.
고기의 개수 N과 사람의 수 M을 입력 받습니다. 다음으로 N번 반복을 통해 고기의 시작 s, 고기의 끝 e, 고기의 맛 t를 입력 받습니다. 고기의 시작 값을 저장할 sidx를 입력 받습니다. arr, sidx를 정렬하여 고기의 시작값으로 정렬하였습니다. arr은 세그먼트 트리를 만들 것이고, sidx는 이분 탐색으로 세그먼트 트리를 탐색할 범위를 찾을 것입니다.
트리의 크기 지정
size = 1
while size <= N:
size <<= 1
tree = [0] * (2 * size)
arr_idx = [0] * (2 * size)
트리의 크기는 보통 4 * N으로 해도 되지만 지금은 바텀업 세그먼트 트리를 사용할 것이기 때문에 크기를 정확하게 만들어 주었습니다. 바텀업 세그먼트 트리에 대해 잘 모른다면 다빈치 코딩 바텀업 세그먼트 트리 에서 확인해 보시기 바랍니다. 바텀업 세그먼트 트리를 사용하는 이유는 재귀를 사용하지 않아 더 빠르고, 탐색하는 로직이 없어 업데이트 부분도 빠르게 작동이 가능합니다.
update 함수 만들기
def update(i):
while i:
ii = 2 * i + (1 if tree[2 * i] < tree[2 * i + 1] else 0)
tree[i] = tree[ii]
arr_idx[i] = arr_idx[ii]
i //= 2
for i in range(N):
idx = i + size
tree[idx] = arr[i][1]
arr_idx[idx] = i
update(idx // 2)
먼저 밑의 for 문을 보겠습니다. 인덱스 i값에 size를 더해 트리의 말단에 위치시켜 줍니다. 그리고 인덱스 값을 기억하기 위해 arr_idx를 만들어 앞에서 만든 트리의 인덱스를 기억하도록 합니다. 말단을 지정하고 나면 상위 노드들을 업데이트 합니다. 상위 노드는 자신의 인덱스 값을 1/2 해준 값이 됩니다.
update문은 i값이 0이 될 때까지 반복을 합니다. 업데이트는 최대값을 구하는 것입니다. 따라서 자신의 하위 노드 (2 * i)와 (2 * i + 1) 의 값을 비교하여 더 큰 값을 가져갑니다. (2 * i + 1)이 더 크면 ii 값이 (2 * i + 1)이 되고, (2 * i)가 더 크면 ii값이 (2 * i)가 됩니다.
트리와 arr_idx 값을 기억하여 모든 트리를 업데이트 해줍니다.
query 함수 만들기
query(x, y) 함수는 0부터 x까지의 범위 내에서 y보다 큰 항목을 찾아주는 함수 입니다. 일반적인 탐색으로는 O(N)의 시간이 걸리지만 세그먼트 트리를 이용하면 O(logN)의 시간이 걸려 더 빠르게 찾을 수 있습니다.
y보다 큰 고기를 찾았으면 해당 고기의 맛을 더해줍니다. 그리고 이 고기는 더이상 사용하지 않기 때문에 -1로 업데이트 합니다. 이 과정을 y보다 큰 고기들이 남지 않을 때까지 계속 진행 합니다. 그럼 해당 내용을 코드로 표현해 보겠습니다.
def query(x, y):
ans = 0
while True:
idx = x + size
ai = -1
while idx:
if idx & 1 == 0:
if y <= tree[idx]:
ai = arr_idx[idx]
break
idx -= 1
idx //= 2
if ai < 0:
break
ans += arr[ai][2]
ai += size
tree[ai] = -1
update(ai // 2)
return ans
x는 범위의 끝인 right입니다. y는 꼬치의 위치로 y보다 큰 고기들을 찾는 것입니다. 세그먼트 트리의 탐색을 통해 노드를 찾고 해당 노드의 원래 인덱스 ai를 찾습니다. ai는 arr_idx의 약자 입니다. ai를 통해 원래 고기맛을 더해주고 해당 노드의 값을 -1로 업데이트 합니다. y보다 큰 고기가 더이상 없으면 while문을 빠져 나옵니다. 그리고 모든 고기 맛을 더한 ans 값을 리턴해주면 됩니다.
고기 맛 찾기
update, query 함수를 모두 만들었으니 꼬치의 입력에 따라 답을 찾는 구문을 만들어 보겠습니다.
먼저 이분 탐색을 통해 탐색의 끝 값들을 찾습니다. sidx에서 x보다 큰 첫 번째 항목, y보다 첫 번째 큰 항목을 찾습니다. 해당 인덱스 값보다 1 작은 값으로 px, py값을 지정합니다. 1 작은 값으로 한 이유는 bisect_right값이 찾는 위치의 다음 위치를 리턴하기 떄문입니다. 잘 이해가 되지 않는다면 다빈치코딩 알고리즘 이분탐색을 확인해 보시기 바랍니다.
시작 위치가 x보다 작은 항목들 중 y보다 큰 항목을 찾습니다. 그것들이 양쪽 모두 꼬치가 꽂힌 고기들 입니다. 해당 고기들의 맛을 모두 더해서 출력하면 됩니다. query 문 안의 update를 통해 양쪽 꼬치 모두 꽂힌 고기들이 모두 삭제가 됩니다.
다음으로 x보다 작은 항목들 중 x + 1 보다 큰 고기들을 삭제합니다. 이것은 왼쪽 꼬치에 꽂힌 고기들 입니다. 어짜피 양쪽 꼬치에 꽂힌 항목들은 이전 query에서 제거되었기 때문에 y보다 큰 항목이 있을 것이라는 걱정은 하지 않아도 됩니다. 이 항목들의 고기 맛을 출력할 필요가 없습니다. 그냥 삭제 용도 입니다.
다음으로 y보다 작은 항목들 중 y + 1보다 큰 고기들을 삭제합니다. 이것은 오른쪽 꼬치에 꽂힌 고기들 입니다. 위와 마찬가지 이유로 삭제만 하는 것입니다. 해당 내용을 코드로 작성해 보겠습니다.
from bisect import bisect_right
for _ in range(M):
x, y = mii()
px = bisect_right(sidx, x) - 1
py = bisect_right(sidx, y) - 1
print(query(px, y + 1))
query(px, x + 1)
query(py, y + 1)
모든 코드의 작성이 끝났습니다. 전체 코드를 확인해 보도록 하겠습니다.
전체 코드
import sys
from bisect import bisect_right
input = sys.stdin.readline
mii = lambda : map(int, input().split())
N, M = mii()
arr = []
sidx = []
for _ in range(N):
s, e, t = mii()
arr.append((s, e, t))
sidx.append(s)
arr.sort()
sidx.sort()
size = 1
while size <= N:
size <<= 1
tree = [0] * (2 * size)
arr_idx = [0] * (2 * size)
def update(i):
while i:
ii = 2 * i + (1 if tree[2 * i] < tree[2 * i + 1] else 0)
tree[i] = tree[ii]
arr_idx[i] = arr_idx[ii]
i //= 2
for i in range(N):
idx = i + size
tree[idx] = arr[i][1]
arr_idx[idx] = i
update(idx // 2)
def query(x, y):
ans = 0
while True:
idx = x + size
ai = -1
while idx:
if idx & 1 == 0:
if y <= tree[idx]:
ai = arr_idx[idx]
break
idx -= 1
idx //= 2
if ai < 0:
break
ans += arr[ai][2]
ai += size
tree[ai] = -1
update(ai // 2)
return ans
for _ in range(M):
x, y = mii()
px = bisect_right(sidx, x) - 1
py = bisect_right(sidx, y) - 1
print(query(px, y + 1))
query(px, x + 1)
query(py, y + 1)
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 28219] 2023 정올 1차 주유소 (1) | 2023.08.23 |
|---|---|
| [백준 1655] 가운데를 말해요 (0) | 2023.08.22 |
| [백준 25402] 2022 정올 트리와 쿼리 (0) | 2023.08.18 |
| [백준 22344] 2021 정올 그래프 균형 맞추기 (0) | 2023.08.16 |
| [백준 21762] 2021 정올 공통 부분 수열 확장 (0) | 2023.08.15 |



