목차
2024년도 정보올림피아드 1차대회 필기 초등부 6번부터 10번까지 문제 풀이 입니다.
6번

205명이 3명의 후보에게 투표할 수 있기 때문에 3으로 나눠보면 68명씩 투표할 수 있고 1명이 남게 됩니다. 즉 A, B, C가 68표씩 득표 했다면 지금까지 204명이 투표를 한 것이고, 이제 마지막 한 명을 얻으면 득표수와 무관하게 반드시 당선이 되게 됩니다. 결국 최소 69표를 얻으면 당선이 됩니다.
만약 A가 69표를 얻었다면 B나 C가 1등이 되더라도 2등으로 당선이 됩니다. B가 69표를 얻는다고 하더라도 C는 최대 67표를 얻기 때문에 공동 1등으로 당선이 됩니다. 다른 어떤 경우에도 A는 69표만 있으면 당선이 가능하게 됩니다.
7번

그래프를 보면 왠지 가운데에 위치하고 있는 B가 중심이 되어야 할 것 같습니다. 하지만 이런 문제에 속으면 안됩니다. C나 E나를 중심에 두어도 A와 D를 방문하는데 2개의 간선으로 충분합니다. 이제 C와 E를 연결하는 하나의 간선만 있으면 모든 간선을 2개 이하로 연결할 수 있습니다. 따라서 정답은 1개 입니다.
8번

첫 번째 판을 제외하고 사람이 많이 낸 모양의 이기는 것을 컴퓨터가 내고, 그것을 이기는 것을 내야 합니다. 이것은 결국 현재 낸 모양의 이기는 것이 아닌 지는 모양을 내면 되는 것입니다. 사람이 가장 많이 낸 것이 가위라면 컴퓨터는 그것을 이기는 바위를 낼 것이고, 사람은 다시 그것을 이기는 보자기를 내야하기 때문입니다. 즉 이 규칙을 매 번 생각할 필요 없이 가위한테 지는 보자기를 다음것으로 생각하면 됩니다.
- ( ) 맨 처음 무조건 가위를 내기 때문에 사람은 바위를 내야 합니다.
- (1) 사람이 가장 많이 낸 모양이 바위 하나기 때문에 컴퓨터는 바위를 이길 보자기를 낼 것이고 사람은 가위를 내면 됩니다. 다음부터는 바로 바위에게 지는 가위라고 하겠습니다.
- (1 0) 지금까지 사람이 낸 순서는 바위와 가위의 숫자가 같습니다. 낸 횟수가 같기 때문에 가위를 우선으로 하고 가위에게 지는 보자기를 내면 됩니다.
- (1 0 2) 숫자가 같습니다. 그럼 가위가 우선이 되고, 가위에게 지는 보자기를 내면 됩니다.
- (1 0 2 2) 보가 많습니다. 보에게 지는 바위를 냅니다
- ( 1 0 2 2 1) 바위와 보가 같습니다. 바위를 우선으로 하기 때문에 가위를 냅니다.
- (1 0 2 2 1 0) 숫자가 같습니다. 가위가 우선이 되고, 보를 내면 됩니다.
- (1 0 2 2 1 0 2) 보가 많습니다. 바위를 냅니다.
- (1 0 2 2 1 0 2 1) 8자인 문자열이 되었습니다.
정답인 (1 0 2 2 1 0 2 1)을 찾았습니다. 규칙성을 보았을 때 1 0 2 이후에는 계속 2 1 0을 붙여주면 된다는 것을 알 수 있습니다. 8자가 아닌 더 큰 숫자가 아닌 다른 숫자가 나와도 순서에 맞게 붙여주면 정답을 찾을 수 있습니다.
9번

최소 이동 횟수를 찾기 위해서는 빠르게 숫자가 커져야 합니다. 세 가지중 2i + 1을 사용해서 빠르게 숫자를 키울 수 있습니다. i가 9라면 2 * 9 + 1 로 19가 되고 여기서 19 - 1로 18을 만들 수 있습니다. 이렇게 2번의 횟수를 사용 했습니다.
이제 9를 만드는 방법을 생각해 보겠습니다. i가 4라면 2 * 4 + 1로 9를 만들 수 있습니다. 혹은 i가 7이라면 7 + 2로 9를 만들 수 있습니다.
4와 7을 만드는 방법을 생각해 보겠습니다. 쉽게 만들 수 있을 것 같은 4는 의외로 많은 숫자가 필요합니다. 7은 i가 3일 때 3 * 2 + 1로 7을 만들 수 있습니다. 3은 i + 2, 2i + 1 어느 것을 사용해도 만들 수 있습니다.
이제 1부터 다음의 단계를 사용하면 만들 수 있습니다.
- 1 + 2 = 3
- 3 * 2 + 1 = 7
- 7 + 2 = 9
- 9 * 2 + 1 = 19
- 19 - 1 = 18
이렇게 5번만에 1로 시작하여 18을 만들 수 있습니다. 접근이 쉽지 않다면 DP 처럼 테이블을 그려 찾을 수도 있습니다.
137919
| 1 | 3 | 7 | 9 | 19 | |
| i - 1 | 2 | 6 | 5 | 18 | |
| i + 2 | 3 | 5 | 9 | 11 | |
| 2i + 1 | 3 | 7 | 15 | 19 |
간단하게 1, 3, 7, 9, 19까지만 표현했지만 실제로는 1부터 20까지 그려놓고 진행하는 것을 추천합니다.
10번

최소 신장 트리는 모든 노드들을 연결한 그래프 중 가중치가 가장 작은 경우를 최소 신장 트리라고 합니다. 최소 신장 트리를 구하기 위해서는 크루스칼 알고리즘이나 프림 알고리즘을 사용합니다. 여기서는 크루스칼 알고리즘을 통해 문제를 해결해 보겠습니다. 크루스칼 알고리즘은 다음과 같은 규칙을 가지고 진행합니다.
- 모든 간선들을 오름차순으로 정렬한다.
- 가중치가 작은 간선부터 선택하여 정점들을 연결한다.
- 연결된 정점에서 사이클이 발생한다면 해당 연결은 스킵한다.
- 2~3번을 반복하여 모든 간선이 열결되면 최소 신장 트리를 구할 수 있습니다.
위 알고리즘에 대해 좀 더 알고 싶다면 아래 링크를 통해 확인하시기 바랍니다.
01. 크루스칼 알고리즘
# 크루스칼 알고리즘 크루스칼 알고리즘(Kruskal Algorithm)에 대해 알아보겠습니다. 이 알고리즘은 모든 정점을 포함하고, 사이클이 없는 연결 선을 그렸을 때, 가중치…
wikidocs.net
사이클은 어떤 노드에서 시작해서 자기 자신인 노드로 돌아올 수 있는 경우를 뜻합니다. 즉 간선을 통해 이동하다 회전이 가능하다면 사이클이 생성 되었다고 말할 수 있습니다. 이제 위 규칙대로 진행해 보겠습니다.
먼저 가중치가 가장 작은 A와 F를 연결합니다.
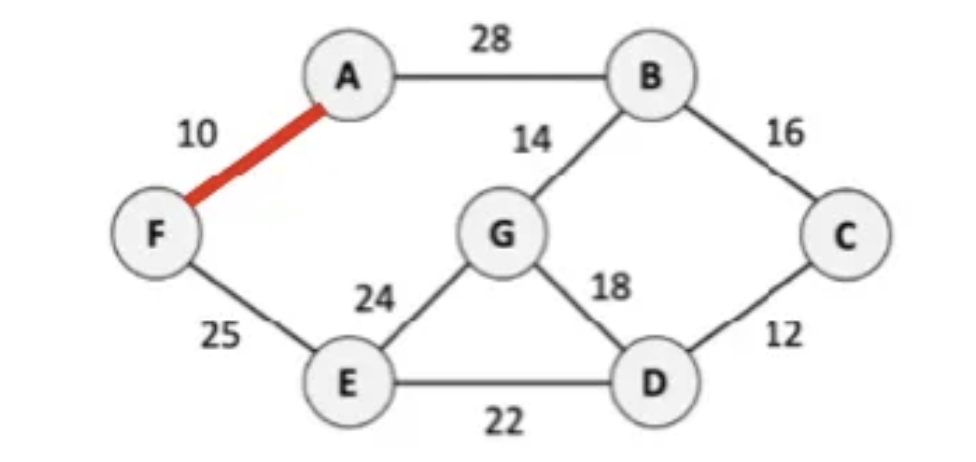
다음으로 숫자가 작은 12인 C와 D를 연결 합니다.
그리고 다음으로 작은 14인 B와 G를 연결 합니다.
다음으로 작은 16인 B와 C도 연결 합니다. 그럼 아래와 같은 모습이 됩니다.

이제 다음으로 작은 18인 D와 G를 연결해야 하는데 이 간선을 연결하면 사이클이 생성됩니다. 따라서 이 간선은 놔두고 다음으로 넘어갑니다. 다음은 22인 D와 E를 연결한 간선 입니다.

다음으로 작은 E와 G를 연결하면 사이클이 생기기 때문에 다음으로 넘어갑니다. 마지막으로 E와 F를 연결하면 최소 신장 트리를 구할 수 있습니다. 마지막 28인 A와 B 역시 사이클이 생성되기 때문에 넘어갑니다.

이제 사용된 간선들의 합을 구합니다.
- 10 + 12 + 14 + 16 + 22 + 25 = 99
이렇게 간선들의 합 99를 구할 수 있습니다.
'알고리즘 설명 > 정보올림피아드 필기' 카테고리의 다른 글
| 2024년 정보올림피아드 필기 초등부(16 ~ 20) (0) | 2025.03.27 |
|---|---|
| 2024년 정보올림피아드 필기 초등부(11 ~ 15) (0) | 2025.03.21 |
| 2024년 정보올림피아드 필기 초등부(1 ~ 5) (0) | 2025.03.17 |
| 2023년 정보올림피아드 필기 중등부(16 ~ 20) (2) | 2024.04.26 |
| 2023년 정보올림피아드 필기 중등부(11 ~ 15) (1) | 2024.04.25 |



