목차
2024년도 정보올림피아드 1차대회 필기 초등부 11번부터 15번까지 문제 풀이 입니다.
11번

인버전의 개수라는 용어에서 Inversion Counting 알고리즘이 생각나야 합니다. 이 알고리즘은 역순으로 되어 있는 순서쌍의 개수를 세는 알고리즘입니다. 자세한 설명은 아래 링크 확인 바랍니다.
https://davincicoding.tistory.com/22
Inversion Counting 알고리즘
Inversion Counting 이란? Inversion Counting 이란 역순으로 되어 있는 순서쌍의 개수를 세는 유명한 알고리즘 입니다. 쉽게 예를 들면 아래와 같은 숫자가 있습니다. 3 2 5 4 1 이렇게 5개의 숫자가 있습니다
davincicoding.co.kr
이 문제에서는 어떻게 사용되는지 알아보겠습니다. 먼저 i값이 1의 경우 Ci는 0 입니다. 이는 왼쪽에 자신보다 큰 숫자가 하나도 없다는 뜻입니다. 다음으로 2의 경우는 왼쪽에 자신보다 큰 숫자가 1개 있다는 뜻입니다. 즉 i를 기준으로 Ci는 자신보다 큰 숫자들이 왼쪽에 몇개 있는지를 찾으면 되는 문제 입니다.
위 로직대로 생각하면 5번째 자리에 가장 큰 숫자인 8이 옵니다. 그래야 5의 위치에서 왼쪽에 해당 숫자보다 큰 숫자가 없다는 0을 만족하기 때문 입니다.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ci | 0 | 1 | 0 | 3 | 0 | 5 | 2 | 3 |
| Ai | 8 |
다음으로 i값이 3인 경우 Ci가 0이기 때문에 그 위치가 7이 됩니다. i가 6, 7, 8에 1이 있었다면 7이 들어갈 수도 있었겠지만 6, 7, 8에 1이 없기 때문에 3의 위치에 넣어주면 됩니다.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ci | 0 | 1 | 0 | 3 | 0 | 5 | 2 | 3 |
| Ai | 7 | 8 |
다음으로 7의 위치에 6이 들어 갑니다. 위와 마찬가지로 i가 1인 위치에 6이 들어가도 되지 않을까 생각할 수 있는데 그렇게 하면 다른 숫자들이 맞지 않습니다. 다른 숫자가 들어갈 수 있는지도 생각해야 합니다.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ci | 0 | 1 | 0 | 3 | 0 | 5 | 2 | 3 |
| Ai | 7 | 8 | 6 |
이와 같은 방식으로 숫자들의 관계를 생각해서 숫자를 배치하다보면 아래와 같은 결과를 얻을 수 있습니다.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ci | 0 | 1 | 0 | 3 | 0 | 5 | 2 | 3 |
| Ai | 4 | 3 | 7 | 2 | 8 | 1 | 6 | 5 |
따라서 결과는 4 3 7 2 8 1 6 5 를 얻을 수 있습니다.
12번

그래프를 잘 확인해보면 9 → 2 → 5 → 4 → 8 → 9 순으로 사이클이 형성되어 있음을 알 수 있습니다. 5나 9가 되기 위해서는 이 사이클에 들어와서 5의 배수만큼 돌면 원래 자기 자리로 돌아오게 됩니다. 이것을 알고 있으면 101번씩 계산할 필요가 없습니다. 사이클에 속해있는 2나 8의 경우 5의 배수인 100번을 지나면 자기 자신의 위치로 되돌아오고 이제 한 칸씩만 더 가면 5와 9에 도착 가능합니다. 즉 101번의 이동으로 5 또는 9가 된 것입니다.
이제 우리가 찾을 것은 2나 8에 5의 배수로 도착 가능한 정점들 입니다. 5의 배수 안에 2나 8에 도착한다면 사이클이 돌고 101번째에 5나 9에 도착 가능하기 때문 입니다.
먼저 2를 생각해 보겠습니다. 사이클을 통하지 않고 2를 5번 이동해서 도착 가능한 정점은 없습니다. 대신 8에서 2번을 지나면 2에 도착 가능합니다. 그럼 결국 8에 언제 도착 가능한지만 찾으면 됩니다.
- 8에 5번 이동에 도착 가능한 정점
- 8에 3번 이동에 도착 가능한 정점
이렇게 두 가지 경우로 나눌 수 있습니다.
8에 5번만에 도착 가능한 정점은 3, 14, 12 입니다.
다음으로 8에 3번만에 도착 가능한 정점은 6, 10 입니다.
이렇게 찾은 2, 8, 3, 14, 12, 6, 10 의 모든 합은 55가 됩니다.
13번

21번만의 이동으로 최대한 많은 과일을 가져가야 합니다. 전체를 모든 과일을 먹기 위해서는 왼쪽으로 12만큼 갔다가 오른쪽으로 14만큼 가야 하기 때문에 21번안에 모든 과일을 먹을 수는 없습니다. 끝까지 다 갈 수는 없기 때문에 최대한 적은 거리로 오른쪽이나 왼쪽을 갔다가 반대로 되돌아 오는 경로를 찾아야 합니다.
왼쪽 -6에 위치한 과일까지 먹고 오른쪽으로 돌아간다면 20번 이동으로 5개의 과일을 획득할 수 있습니다. 이 방법이 과일을 가장 많이 먹을 수 있는 방법입니다.
14번

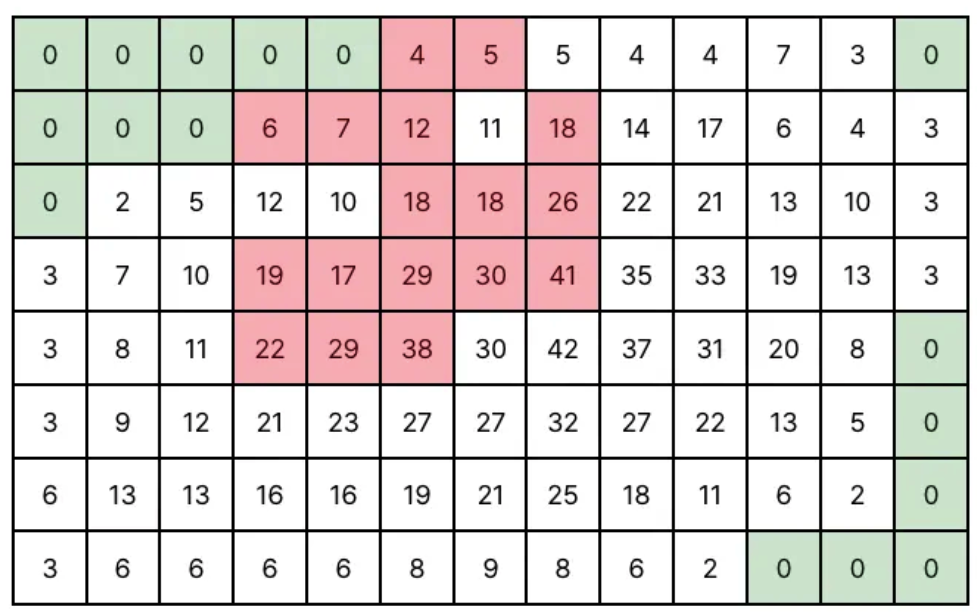
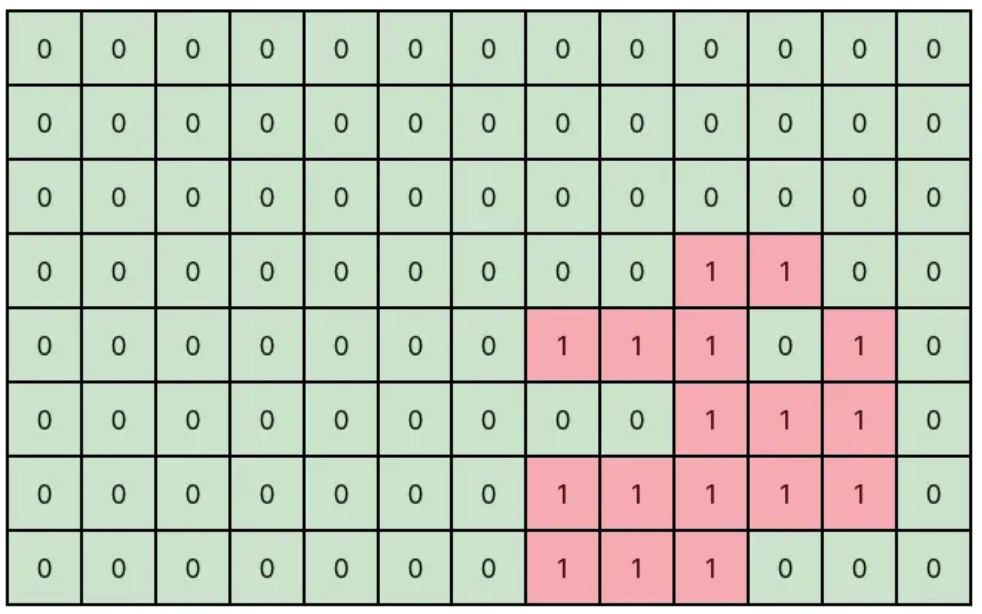
시뮬레이션 문제 입니다. 어렵게 생각할 필요 없이 맨 위쪽, 왼쪽부터 차례로 숫자가 0이 될 때까지 클릭하면서 이동하면 자연스럽게 문제가 해결 됩니다.

15번

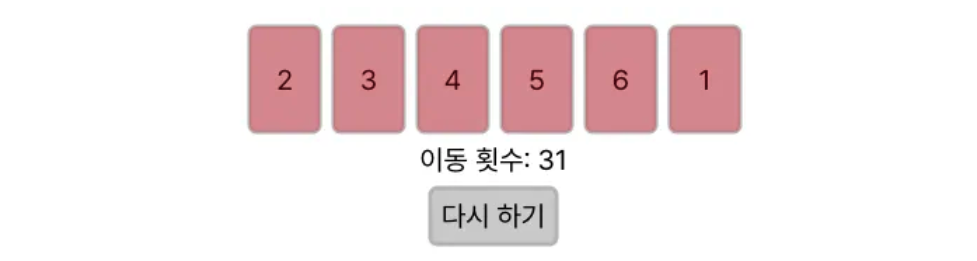
숫자가 제자리 카드가 되었을 때에만 이동이 가능합니다. 이동 가능한 숫자들 중 가장 앞에 있는 숫자만 선택해서 이동시키면 문제를 해결할 수 있습니다.
'알고리즘 설명 > 정보올림피아드 필기' 카테고리의 다른 글
| 2024년 정보올림피아드 필기 초등부(16 ~ 20) (0) | 2025.03.27 |
|---|---|
| 2024년 정보올림피아드 필기 초등부(6 ~ 10) (0) | 2025.03.19 |
| 2024년 정보올림피아드 필기 초등부(1 ~ 5) (0) | 2025.03.17 |
| 2023년 정보올림피아드 필기 중등부(16 ~ 20) (2) | 2024.04.26 |
| 2023년 정보올림피아드 필기 중등부(11 ~ 15) (1) | 2024.04.25 |



