목차
문제 출처 : https://www.acmicpc.net/problem/13306
트리(13306)
이 문제는 2016년 정보올림피아드 중등부 3번 문제 입니다.
문제 이해하기
트리가 구성되어 있고, 이 트리를 자른 다음 두 정점이 연결되어 있는지를 파악하는 문제 입니다. 예제 입력 2를 보겠습니다. 입력된 정점들을 모두 연결하면 본문에 나와 있는 트리 형태가 됩니다.

이제 N - 1개의 (1)번 형태의 쿼리와, Q개의 (2)번 형태의 쿼리가 주어집니다. 0으로 시작하는 (1)번 쿼리는 연결된 정점을 삭제합니다. 첫 번째 쿼리인 (0 11)은 11번 정점의 연결을 삭제합니다.

다음 쿼리 (1 8 5)는 8과 5의 연결 여부를 확인합니다. 11번 정점의 연결이 삭제되어 8과 5는 연결이 안되어 있다는 것을 알 수 있습니다. 다음으로 (1 3 9) 쿼리는 3과 9의 연결을 확인합니다. 두 정점은 연결되어 있음을 알 수 있습니다.
다음으로 (0 10), (0 9), (0 7)은 10번 9번, 7번의 연결을 삭제합니다.
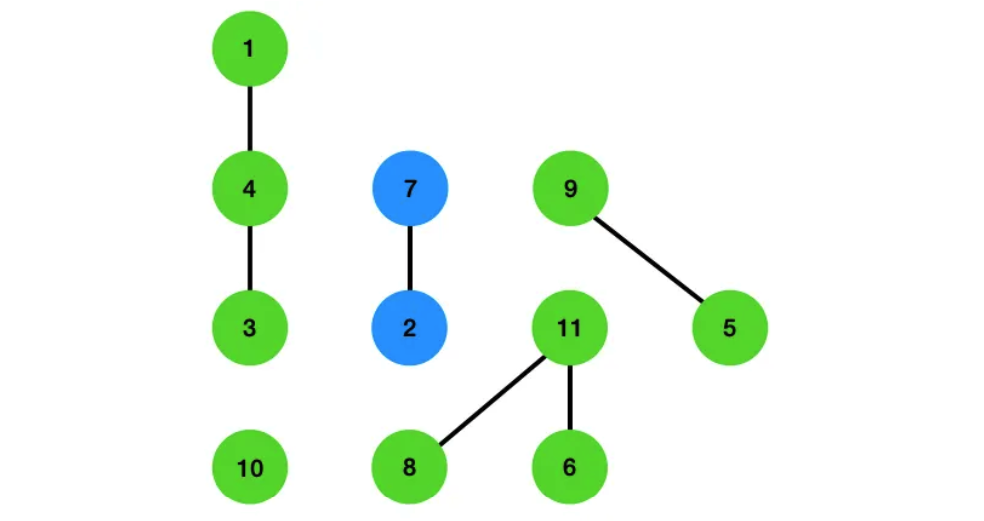
삭제 후 (1 2 7) 쿼리로 2번과 7번의 연결을 확인 합니다. 두 정점이 연결 되어 있음을 알 수 있습니다. 그 이후에도 삭제하는 쿼리와 확인하는 쿼리로 삭제와 확인을 반복합니다.
이렇게 모든 쿼리를 수행하면 모든 연결이 끊겨있는 것을 볼 수 있습니다.

여기서 왜 삭제 쿼리가 N - 1개이고, 확인하는 쿼리가 Q개인지 알 수 있습니다. N - 1이라는 숫자는 트리의 정점에 연결되어 있는 모든 간선을 뜻합니다. 즉 하나하나 삭제해 나가면서 모든 연결이 끝날때까지 진행한다는 뜻입니다.
잘 생각해보면 모든 트리에서 정점이 N개라면 간선의 개수는 N - 1개라는 사실을 알 수 있습니다.
그럼 이 문제에서 주어진 두 가지 쿼리의 의미를 거꾸로 생각한다면 문제를 쉽게 해결할 수 있습니다.
- 트리의 간선을 모든 연결이 끊길 때까지 하나씩 제거한다.
- 트리의 연결 정보를 확인한다.
이 문제를 뒤집어서 생각하면 다음과 같습니다. 모든 쿼리를 거꾸로 진행한다면 다음과 같은 문제가 됩니다.
- 트리의 각각의 정점을 하나씩 연결한다.
- 트리의 연결 정보를 확인한다.
이렇게만 설명하면 어려울 수 있기 때문에 예제를 다시 한 번 보겠습니다. 마지막 쿼리 (0 4)와 그 이전 쿼리 (0 3)은 각각 3번의 연결을 끊고, 4번의 연결을 끊는 쿼리입니다. 원래는 연결되어 있었을 간선을 삭제하는 쿼리이기 때문에 반대로 진행한다면 4번을 연결하고, 3번을 연결하는 쿼리가 됩니다.

이제 그 위 쿼리 (1 1 3)은 1번과 3번이 연결되어 있음을 확인하는 쿼리 입니다. 1번과 3번 정점이 연결되어 있음을 알 수 있습니다. 다음인 (0 2), (0 6), (0 8)은 2, 6, 8번을 다시 연결합니다.

그 위 쿼리 (1 1 10)은 1번과 10번이 연결 되어 있음을 묻고 있습니다. 우리는 두 정점이 끊겨 있는것을 알 수 있습니다.
문제를 거꾸로 진행하니 우리에게 익숙한 문제임을 알 수 있습니다. 바로 분리 집합 유니온 파인드 입니다. 유니온 파인드에 대해 잘 모른다면 아래 링크를 통해 유니온 파인드에 대해 확인해 보시기 바랍니다.
02. 유니온 파인드
# 유니온 파인드 분리 집합으로 불리는 유니온 파인드(Union Find)는 그래프 형태의 자료들의 연결 정보를 알고 싶을 때 사용합니다. 란?
이런 형태의 알고리즘을 오프라인 쿼리라고 합니다. 보통 유니온 파인드의 경우 연결 여부를 즉각적으로 반환 합니다. 이렇게 유니온 파인드나, 세그먼트 트리 문제의 경우 즉각적인 반응을 온라인 쿼리라 하고, 즉각적으로 반응하지 않아도 되는 경우나 데이터가 고정적이라 업데이트가 없는 경우, 쿼리 간 의존성이 없는 경우에 쿼리를 일괄적으로 처리하거나, 쿼리의 순서를 재정렬하여 최적화 하는 경우에 오프라인 쿼리라고 합니다.
이 문제의 경우 쿼리의 순서를 뒤집어 거꾸로 수행하고, 결과 역시 거꾸로 하여 한번에 보여주면 되기 때문에 오프라인 쿼리라 할 수 있습니다.
코드 작성하기
그럼 코드를 작성해 보겠습니다.
입력 받기
mii = lambda : map(int, input().split())
N, Q = mii()
parents = [1] * (N + 1)
for i in range(2, N + 1):
parents[i] = int(input())
queries = []
for _ in range(N - 1 + Q):
queries.append(tuple(mii()))
정점의 개수 N과 질의의 개수 Q를 입력 받습니다. 다음으로 N - 1개의 줄에 부모 정점을 입력 받습니다. 1번은 루트이고 2번 정점부터 부모가 누구인지 받게 됩니다.
다음으로 N - 1 + Q개의 줄에 쿼리를 입력 받습니다. 쿼리는 0으로 시작하는 삭제 쿼리와 1로 시작하는 연결 확인 쿼리로 되어 있습니다.
유니온 파인드
유니온 파인드의 두 함수를 구현합니다.
p = list(range(N + 1))
def find(a):
if a != p[a]:
p[a] = find(p[a])
return p[a]
def union(a, b):
pa = find(a)
pb = find(b)
p[pb] = pa
앞서 parents 리스트를 통해 이미 부모 정보를 입력 받았지만 p라는 부모 리스트를 따로 만들어 주었습니다. 우리는 오프라인 쿼리로 모두 삭제된 정점을 새로 연결한다고 했습니다. 즉 parents는 마지막 연결 정보이고, 유니온 파인드를 통해 연결될 정보는 다시 구성해야 한다는 뜻입니다. 그래서 유니온 파인드로 연결할 부모 정보가 바로 p 리스트 입니다.
유니온 파인드에 함수에 대해서는 위 링크에 설명 되어 있어 따로 더 설명하지 않겠습니다.
오프라인 쿼리 수행
ans = []
for query in queries[::-1]:
if query[0] == 0:
a = query[1]
b = parents[a]
union(a, b)
else:
a, b = query[1:]
rst = "NO"
if find(a) == find(b):
rst = "YES"
ans.append(rst)
print(*ans[::-1], sep="\\n")
입력 받은 쿼리 queries를 전부 뒤집기 위해 슬라이싱처리 하였습니다. 슬라이싱이 어색하다면 reversed(queries)를 사용해도 상관 없습니다.
쿼리의 첫 번째 값이 0인경우는 원래 삭제를 하는 것이고, 1번의 경우는 연결을 확인하는 것이였습니다. 이제 거꾸로 수행하기 때문에 0인 경우에 두 정점을 연결하고, 1인 경우에 연결을 확인하는 것입니다. 우리는 결과 ans 역시 뒤집어서 출력해야 하기 때문에 결과를 ans 리스트에 담아줍니다.
모든 쿼리를 수행한 뒤 ans의 결과를 뒤집어 주고, 각 결과를 한 줄에 하나씩 출력하기 위해 sep에 “\n” 를 사용하여 출력합니다.
전체 코드
그럼 전체 코드를 확인해 보겠습니다. 전체 코드에는 속도 향상을 위해 sys.stdin.readline 을 사용하였고, 유니온 파인드를 사용하기 위해 재귀함수의 한계를 늘려 주었습니다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10 ** 5)
mii = lambda : map(int, input().split())
N, Q = mii()
parents = [1] * (N + 1)
for i in range(2, N + 1):
parents[i] = int(input())
queries = []
for _ in range(N - 1 + Q):
queries.append(tuple(mii()))
p = list(range(N + 1))
def find(a):
if a != p[a]:
p[a] = find(p[a])
return p[a]
def union(a, b):
pa = find(a)
pb = find(b)
p[pb] = pa
ans = []
for query in queries[::-1]:
if query[0] == 0:
a = query[1]
b = parents[a]
union(a, b)
else:
a, b = query[1:]
rst = "NO"
if find(a) == find(b):
rst = "YES"
ans.append(rst)
print(*ans[::-1], sep="\\n")
'알고리즘 문제 풀이' 카테고리의 다른 글
| [백준 31965] 회의 장소 (1) | 2025.06.24 |
|---|---|
| [백준 7573] 고기잡이 (2) | 2025.01.27 |
| [백준 10211] Maximum Subarray (0) | 2025.01.19 |
| [백준 1149] RGB 거리 (0) | 2024.12.07 |
| [백준 24552] 올바른 괄호 (4) | 2024.11.27 |


